Утверждение:
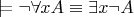
Мое доказательство:
Пусть

- произвольная модель языка, а

- произвольная оценка для нашей формулы.
Нужно доказать
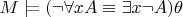
.
Пусть
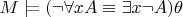
.
Так как

не входит свободно в
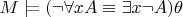
, то пусть
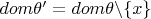
и
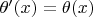
для всех
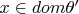
.
Согласно п. 2 § 2 гл. 2
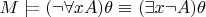
.
Согласно п. 2 § 2 гл. 2
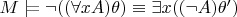
.
Согласно п. 2 § 2 гл. 2
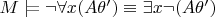
.
Согласно п. 5 и п. 6 § 3 гл. 2 пусть
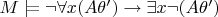
.
Согласно п. 5 § 3 гл. 2 положим
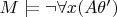
.
Тогда согласно п. 5 § 3 гл. 2 нужно доказать
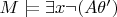
.
Поскольку
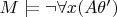
, то неверно, что
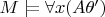
.
Значит неверно, что для любого объекта

из области соответствующего сорта
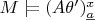
.
Следовательно, существует

, такое, что неверно
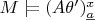
, что означает
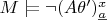
.
Тогда согласно п. 5 § 3 гл. 2
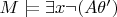
.
Следовательно
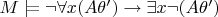
.
Согласно п. 5 и п. 6 § 3 гл. 2 пусть
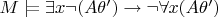
.
Согласно п. 5 § 3 гл. 2 положим
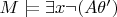
.
Тогда согласно п. 5 § 3 гл. 2 нужно доказать
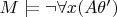
.
Поскольку
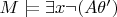
, то существует

из области соответствующего сорта
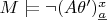
, а значит для этого

неверно, что
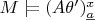
.
Поэтому неверно, что для любого

верно
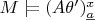
.
Тогда согласно п. 5 § 3 гл. 2
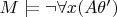
.
Следовательно
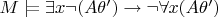
.
Так как
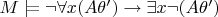
и
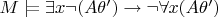
, то согласно п. 5 и п. 6 § 3 гл. 2
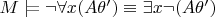
и соответственно
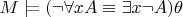
.
Так как
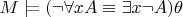
для любой произвольно выбранной модели

и оценки

, то
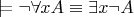
 Основные определения из книги Колмогоров А.Н. Драгалин А.Г. Введение в математическую логику 1982:
Основные определения из книги Колмогоров А.Н. Драгалин А.Г. Введение в математическую логику 1982:Модель

п. 3 § 3 гл. 2.
Оценка

для выражения

п. 2 § 3 гл. 2.
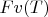
п. 10 § 1 гл. 2.
Вопросы:В1: Верно ли доказательство?
В2: Если ответ на В1 положительный, то можно ли считать его достаточно строгим? (
это главный вопрос топика)
P.S. Если по каким-то определениям есть вопросы, а в книге сходу не нашли, то спрашивайте, так как я не все определения дал расчитывая на их общеизвестность и экономию своего времени (переписывать целые абзацы очень долго).