Уравнение

[MMyaf]

Решить уравнение в области вещественных чисел:
$(1 - x) ^k - 2 x^k = 2( n - 1 ) $, где $k\in N$, $n\in N$.

[Руст]

Если ограничиться положительными х задача легко решается. Отрицательные решения имеются почти всегда и их не так просто выразить в виде формул при k>2.

[MMyaf]

Цитата:

Если ограничиться положительными х задача легко решается

К сожалению, не вижу насколько легко. Что за метод применять?
Может $(1-x)^k$ разложить по биномиальной формуле Ньютона?
Но даже при такой постановке задачи не вижу дальнейших действий

[Руст]

Положительное решение имеется только при n=1, т.е $(\frac{1-x}{x})=2^{1/k}.$

[MMyaf]

Дело в том, что это уравнение возникло в процессе решения вот какой задачи:
Пусть $|X|=m$($m\in \mathbb{N}). Доказать,что $(X,\delta)\subset_{iso}(\mathbb{R}^n,\sigma_k)$, где m\leqslant n+1,
$\delta(x,y)=$ $ \left\{ \begin{array}{l} 0,x=y,\\ 1,x\neq y, \end{array} \right. $при x,y \in X и
$\sigma_k(x,y)=\sqrt[k]{\sum_i^n|x_i-y_i|^k}$, при $x,y \in \mathbb{R}^n$.Т.е. нужно показать, что метрическое пространство $(X,\delta)$ является изометричным вложение в метрическое пространство $(\mathbb{R}^n,\sigma_k)$.
Пусть $a_i \in X$ для $i=1,m$. Далее
$(X,\delta)\subset_{iso}(\mathbb{R}^n,\sigma_k)$:$ \left\{ \begin{array}{l} a_1 \to x_1=(\frac{1}{\sqrt[k]{2}},0,...,0)\\ a_2 \to x_2=(0,\frac{1}{\sqrt[k]{2}},0,...,0)\\ ... \\ a_n \to x_n=(0,0,...,0,\frac{1}{\sqrt[k]{2}})\\ a_{n+1} \to x_{n+1}=(\alpha,\alpha,...,\alpha)\\ \end{array} \right. $
Для полного построения необходимо найти $\alpha.
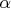
$\delta(a_{n+1},a_i)=\sigma_k(x_{n+1},x_i)$,при $i=1,n $
$1=\sqrt[k]{(n-1)|\alpha^k|+|\alpha-\frac{1}{\sqrt[k]{2}}|^k}$. Вот это уравнение и вызвало вопрос. После нескольких замен это уравнение свелось к такому:
$(1-x)^k-2x^k=2(n-1)$. Необходимо найти одно из решений $\alpha=f(k,n)$.