Сначала привожу цитату из книги с моим вопросом, а ниже почти все необходимые определения из книги.
Есть вопрос по пункту
7 §2 главы 2 книги Колмогорова, Драгалина "Введение в математическую логику" (если понадобится, то её можно скачать вот
тут):
Цитата:
7. Пусть

- формула и

- подстановка, необязательно допустимая для

. Как мы уже говорили, в этом случае

, вообще говоря, непригодна с точки зрения предполагаемого смысла подстановки. Правильный способ действий в этой ситуации таков. Следует найти вариант

,

, такой, что

допустима для

, и рассмотреть формулу

. Мы назовем

результатом
правильной подстановки 
в

и обозначим

через
![$[A \theta]$ $[A \theta]$](https://dxdy-03.korotkov.co.uk/f/e/a/4/ea4f165d9f43fbf072769613233c475c82.png)
.
Формула
![$[A \theta]$ $[A \theta]$](https://dxdy-03.korotkov.co.uk/f/e/a/4/ea4f165d9f43fbf072769613233c475c82.png)
определена неоднозначно, она зависит от выбора варианта

. Однако если

и

- подстановка, свободная для

и для

, то

. Таким образом, правильная подстановка определена однозначно с точностью до конгруэнтности.
То обстоятельство, что нужный вариант

, для которого

допустима, найдется, вытекает, например, из следующей леммы.
Будем говорить, что формула

обладает
свойством чистоты переменных, если, во-первых, все ее связанные переменные отличны от свободных и, во-вторых, любые два различные вхождения кванторных приставок связывают различные переменные.
Лемма (о чистоте переменных). Пусть  - формула и
- формула и  - конечное множество переменных. Тогда может быть построена формула
- конечное множество переменных. Тогда может быть построена формула  со свойством чистоты переменных такая, что
со свойством чистоты переменных такая, что  и всякая связанная переменная
и всякая связанная переменная  отлична от переменных из множества
отлична от переменных из множества  .
. Вопрос: Зачем вообще вводить
свойство чистоты переменных, если требуется только то, что бы для любого

терм

не содержал свободных переменных, которые могли бы стать связанными попав в область действия одного из кванторов в выражении

, тем более что конечное множество

тут играет роль

(где

множество всех

)?
ОПРЕДЕЛЕНИЯ:Определение
связанной переменной из
8 §1 главы 2:
Цитата:
8. В формулах вида

,

выражение

или

называется
кванторной приставкой,

-
переменной кванторной приставки, а формула

-
областью действия квванторной приставки.
Каждое вхождение переменной в формулу мы будем называть
свободным или
связанным. А именно, вхождение переменной

в формулу

называется связанным, если в

входит формула вида

, причем рассматриваемое вхождение

в

является вхождением

в эту формулу

.
Определение из
8 §1 главы 2 того,
что переменные терма входят в него свободно:
Цитата:
В атомарную формулу всякая переменная по определению входит свободно. Удобно также считать по определению, что все переменные, входящие в терм, входят в него свободно.
Определение

из
9 §1 главы 2:
Цитата:
10. Переменная

называется свободной переменной формулы

, или
параметром 
, если

входит (хотя бы один раз) свободно в

. Разумеется, при этом

может входить в

и связанно.
Множество всех параметров

обозначим через

.
Определение
конгруэнтности (т.е. бинарного отношения обозначаемого

) из
12 §1 главы 2:
Цитата:
12. Уточним теперь, что именно означает ситуация, когда две формулы

и

отличаются друг от друга лишь правильным (т.е. без коллизий переменных) переименованием связанных переменных. В этом случае мы будем говорить, что формулы

и
 конгруэнтны
конгруэнтны, или что формула

является
вариантом формулы

, и писать

.
...
Можно дать и аккуратное математическое определение отношения

индукцией по логической сложности

формулы

. А именно:
А) единственным вариантом атомарной формулы является она сама;
Б) если

имеет вид

, то всякий вариант

формулы

имеет вид

, где

и

;
если

имеет вид

, то всякий вариант

формулы

имеет вид

, где

;
В) если

имеет вид

, то всякий вариант

формулы

имеет вид

, где

и

таковы, что для всякой новой переменной

(т.е. не входящей ни свободно, ни связанно в формулы

и

) имеем

.
Здесь через

обозначен результат замещения всех свободных вхождений переменной

в

на переменную

. Аналогично понимается

.
Определение
формальной подстановки 
из
2 §2 главы 2:
Цитата:
2. Пусть

- выражение языка

(т.е. формула или терм) и

- формальная подстановка

. Через

мы обозначим результат одновременного замещения всех
свободных вхождений переменных

в

на термы

соответственно. Конечно, при этом некоторе

могут и не входить свободно в

. Тогда соответствующие

никуда не подставляются и просто не играют никакой роли. Подчеркнем, что замещаются только
свободные вхождения

в

. Вместо

будем иногда употреблять одно из следующих обозначений:

.
Дадим теперь индуктивный рецепт для вычисления подстановки в формулу. Этот рецепт можно рассматривать и как самостоятельное индуктивное определение подстановки. Можно убедится с помощью индукции, что оно эквивалентно данному ранее определению.
А.

.
Б.

,

.
В.

.
Здесь через

обозначен результат "выбрасывания" переменной

из области определения

, т.е.

есть такая подстановка

, что

и
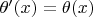
для всякой переменной
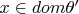
.
Определение
свободной (допустимой) подстановки из
4 §2 главы 2:
Цитата:
4. Заметим теперь, что не все подстановки одинаково пригодны с точки зрения логики.
Пусть, например, в некотором языке атомарная формула

выражает предикат

, где переменные пробегают натуральные числа

. Формула

выражает уже предикат от переменных

и

, а именно

.
Пусть в этом же языке терм

задает операцию умножения натуральных чисел

. Теперь мы желали бы подставить

в

вместо переменной

с целью выразить предикат от трех переменных

. Однако ошибочно было бы рассмотреть с этой целью формулу

, т.е. формулу

. Эта последняя формула выражает совсем имую мысль (в частности, зависимость от двух параметров

и

, а не от трех).
Причина затруднения состоит в том, что переменная

была свободна в терме

, а оказалась связанной в результирующей формуле. Как говорят, произошла
коллизия переменных при подстановке.
Правильный подход состоит в том, что сначала следует переименовать связанную переменную

, например, образовать формулу

, которая выражает тот же предикат, а уже затем произвести подстановку, так что в резульате получим формулу

, которая и выражает нужный предикат.
5. Выделим теперь класс подстановок, которые заведомо не приводят к коллизии переменных.
Подстановка

называется
свободной для выражения 
(или
допустимой для выражения 
), если для всякой переменной

любое свободное вхождение

в

не попадает в область действия кванторов по переменным, свободно входящим в терм

.
Как всегда, мы укажем и индуктивное определение свободной подстановки.
A. Если

- терм или атомарная формула, то всякая подстановка является допустимой для

.
Б.

свободна для



свободна для

и

свободна для

.

свободна для



свободна для

.
В.

свободна для


подстановка

свободна для

, и, кроме того, для всяков переменной

терм

не содержит свободно переменной

.