При решении интеграла

Перепробывал различные способы: под частям, арксинус под знаком дифференциала, подстановки Эйлера.
Впрочем преподаватель сказал использовать подстановки Эйлера, но в новых обозначениях получился "жуткий монстр" в знаметеле с многочленом шестой степени, который имел один корень кратности два равный

. Вот:

А насколько я понимаю (по крайней мере научили меня так) мне надо получить данный многочлен в виде
 (написал коряво, более точно см. Кудрявцев "Курс мат. анализа" том I, параграф 19 пункт 4)
(написал коряво, более точно см. Кудрявцев "Курс мат. анализа" том I, параграф 19 пункт 4)Но не получается упростить сомножитель

Подозреваю, что коэффициент

далеко не целое число...
Полистал Фихтенгольца, наткнулся на подстановки Абеля, помогут ли?
Далее в этой литературе дают совет, что порой удобно заменять

на
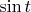
.
После такой замены решаемый мною интеграл принял вид:

Решить его не могу, матпакет Mathematica даёт жуткий ответ с мнимыми единицами...
"Берущийся" ли этот интеграл?
|
i |
zhoraster: |
Не забывайте ставить знаки долларов вокруг формул и обратную косую перед названием стандартной функции:
Код: $\sin t$ |