Подмножество сепарабельного множества тоже сепарабельно

[homo_sapiens]

Столкнулся с такой теоремой не могу доказать и не знаю где найти доказательство. Теорема вроде какая-то известная. Знаю как в частном случае доказать (что множество иррациональных чисел сепарабельно, потому что сдвинув все рациональные числа на sqrt(2) получим всюду плотное множество). Буду благодарен если кто-нибудь подскажет доказательство или укажет источник где можно найти доказательство.

[Dan B-Yallay]

Такие вещи доказываются "по определению".
Дайте определение сепарабельного множества.

[homo_sapiens]

Множество называется сепарабельным, если в нём существует счётное всюду плотное подмножество. В данном случае мне непонятно как это по определению можно доказать

[Dan B-Yallay]

А что означает "всюду плотное"?

[homo_sapiens]

Множество M всюду плотно в X, если для всех EPS > 0 для всех x из X существует y из M что расстояние от x до y < EPS (некрасиво получилось не знаю как здесь формулы вбивать но и так понятно).

[Dan B-Yallay]

Вообще говоря утверждение неверно. Есть контрпримеры. Но если поднможество открытое, тогда верно.

[homo_sapiens]

Если подмножество открытое, то я вроде знаю как доказать. Но утверждение для любого подмножества. Может утверждение и не верно, а какой контрпример?

[Dan B-Yallay]

homo_sapiens писал(а):

, а какой контрпример?

Если с английским дру'жите:
http://en.wikipedia.org/wiki/Sorgenfrey_plane

[homo_sapiens]

Мне наверное стоило уточнить, что исходное множество берётся в метрическом пространстве (подумал что это само собой разумеется)

[Dan B-Yallay]

Тогда давайте так. Пусть $X$ метрическое пространство и $M \subset X$ всюду плотно в $X$. Пусть $U \subset X$
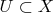
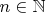
Для каждого $n \in \mathbb N$ строим $1/n$ окрестность возле $\forall m \in M$. Выбираем в каждой такой окрестности элемент из $U$ и обзываем полученное множество точек $M_n$ .

$$M_U= \cup_{n\in \mathbb N} M_n$$

Покажите, что $M_U$ - счетно и плотно в $U$

PS.Конечно мы подразумеваем отктытость $U$

[homo_sapiens]

Вы уверены что данная теорема верна только для открытого подмножества? Просто для открытого я давно придумал доказательство. Но мне нужно доказать для любого подмножества (можете объяснить контрпример я его не очень понял).

[Kallikanzarid]

$X \in \mathsf{Top},\ Y \subset X$ - счетное, всюду плотно в $X$. Для любого $Z \subset X$ постройте счетное множество, всюду плотное в $Z$.