Ну, простые числа и

не являются совершенно стрАшными, поскольку для них один множитель должен быть равен

, а другой - самому этому числу, поэтому сумма будет больше. Число

- совершенно стрАшное, поскольку

. Если число
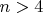
составное, то его можно представить в виде произведения двух натуральных чисел

и
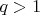
. Тогда

. Добавляя

единичных множителей, получим требуемое представление и в виде суммы, и в виде произведения. Так что совершенно стрАшные натуральные числа - это в точности составные числа.