Помогите решить уравнение

[jrMTH]

$f(x) = -7x^2 + 23x + 23$

Если
$-1 < f'(x) < 1$

Тогда $h < x < k$

Какое значение k? Как решать - не пойму.

[Алексей К.]

Ну так запишите же неравенства с производной в явном виде.

-- 01 май 2011, 11:18 --

Перечитал заголовок. А какое уравнение Вам надо решить?

[oveka]

jrMTH в сообщении #440545 писал(а):

$f(x) = -7x^2 + 23x + 23$
Если $-1 < f'(x) < 1$
Тогда $h < x < k$
Какое значение k? Как решать - не пойму.

Это не уравнение. Это поиск аргумента по значению производной.
Просят найти производную, определить при каких х она равна -1 и +1.
Они (иксы) и будут искомые. Удачи.

[spaits]

Для наглядности нахожу вершину параболы (небольшие по модулю значения производной находятся в в интервале с центром в вершине параболы), хотя это и не нужно для решения задачи: $x_0=\dfrac{23}{14}$. Формулу для нахождения вершины параболы знаете?
Для решения, как уже писали Вам, надо взять производную и подставить в неравенство.
$f'(x)=-14x+23$; $-1<-14x+23<1$; $-24<-14x<-22$; $22<14x<24$; $\dfrac{11}{7}<x<\dfrac{12}{7}$.
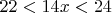
Отсюда Вы сами сможете найти $h$ и $k$? Жду Вашего ответа, чему равны $h$ и $k$!
Обратите внимание, что вершина параболы $x_0=\dfrac{23}{14}$ действительно находится в центре интервала: $\dfrac{11}{7}=\dfrac{22}{14}$; $\dfrac{12}{7}=\dfrac{24}{7}$.