Теория вероятности

[st256]

Я взял случайную величину $x$ и всю ее область значений разделил на $N$ областей

$$x \in \left [ \xi_k, \xi_{k+1} \right ]$$

все значения $x$ на интервале $\left [ \xi_k, \xi_{k+1} \right ]$ я заменил на одно значение $x_k$.

Далее, я попытался найти при каких наборах $\xi_i$ дисперсия величины $x-x_k$ будет наименьшей. Я достаточно быстро пришел к выводу, что должен либо максимизировать выражение

$$ \sum_k M^2_k p_k $$

где $M_k$ - мат. ожидание $x$ на интервале $\left [ \xi_k, \xi_{k+1} \right ]$, а $p_k$ - вероятность того, что $x$ на этот интервал попадет
либо минимизировать

$$ \sum_k D_k p_k $$

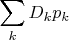
где $D$ - дисперсия $x-x_k$ на интервале $\left [ \xi_k, \xi_{k+1} \right ]$

А вот что делать дальше?...

[ozhigin]

а задача то в чем?

[st256]

Задача в том, чтобы найти такое расположение уровней квантования, при котором среднеквадратичная ошибка квантования имела бы минимум.