Непрерывные функции

[bundos]

Можно ли эту задачу решить, не используя теоремы функана (просто курс у нас ещё не читался).
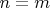
Пусть $\{ f_n\}$ последовательность непрерывных функций на интервале $[0,1]$, такая, что: $\int\limits_0^1f_m(x)f_n(x)=0$, если $n\neq m$ и $\int\limits_0^1f_m(x)f_n(x)=1$, если $n=m$ и $\mathrm{sup}\{|f_n(x)|: x\in[0,1] , n=1,2,\ldots\}<+\infty$. Доказать, что найдётся подпоследовательность $\{ f_{n_k}\}$, такая, что предел $\lim\limits_{k\to\infty}f_{n_k}(x)$ существует для всех $x\in[0,1]$.

[Sonic86]

http://e-science.ru/forum/index.php?s=a ... opic=30348
Я уже 2-й раз замечаю, что Вы и тот товарищ постите одинаковые задачи. В случае, если Вы с ним разные люди, рекомендую скооперироваться, что ли