сходимость к нормальному распределению и выборочное среднее.

[Caran-d'Ache]

Добрый день!
Возник следующий вопрос по мат.статистике.

Есть следующий алгоритм.
Пусть $x$ - результат нелинейного преобразования суммы случайной величины с нормальным распределением и детерминированной функции вещественного переменного.
Пусть функция плотности вероятности $x$ описывается следующим выражением:
$w(x)=\frac{2}{\pi }+\frac{2 a e^{-\frac{a^2}{2}}}{\sqrt{\pi }} \sum _{n=1}^{\infty } \cos (2 n \psi ) \cos (2 n x)\left(I_{n+\frac{1}{2}}\left(\frac{a^2}{2}\right)+I_{n-\frac{1}{2}}\left(\frac{a^2}{2}\right)\right)$,
где $a, \psi$- неслучайные параметры.
Пусть есть набор тестовых (эталонных) функций $u_1, u_2 ... u_N$ и одна исследуемая $\hat{u}$.
Пусть для каждой пары (одна из тестовых и исследуемая) на основе выборки некоторого объёма $N_{\alpha}$ производится оценка величины $\hat{\psi}$ (которая является результатом комбинации истинного значения параметра $\psi$ и шума с указанным выше распределением). Известно, так же, что в отсутствии шума минимум (равный нулю) достигается только для совпадающих тестового и исследуемого объекта.
Пусть в качестве оценки исследуемой функции берётся тот тестовый объект, который минимизирует $\hat{\psi}$.

Первое, что я сделал - попробовал подсчитать моменты сей величины, при заданном распределении.
Для вычисления моментов, я пользуюсь асимптотикой (при большом аргументе) для модифицированных функций Бесселя полуцелого индекса. Оставляя лишь слагаемые порядка $a^{-2}$ (при достаточно большом $a$ это оправдано, и на практике реализуется чаще именно этот случай), получаю, что мат. ожидание равно $|\psi |$. Что в общем-то очень хорошо, т.к. это соответствует истинному значению.
Вопрос первый:
Правильно ли я понимаю, что мат. ожидание величины $\hat{\psi}$ является несмещённой оценкой истинного значения?
С дугой стороны, мне для измерения доступна конечная выборка, объёмом $N_{stat}$.
Т.е. при грамотном выборе объема выборки я смогу с некоторой погрешностью заменить мат. ожидание на выборочное среднее.
(Это хорошо проводится для "удачных" распределений, вроде Гаусса, по ним в книгах говорится много чего хорошего, вроде, того, что они являются эффективными, несмещёнными и т.д. оценками мат.ожидания.) А для такой вот плотности доказать это... хмм... не знаю.
Прав ли я, что для данной плотности нельзя построить эффективной статистики (вроде как ПРВ не принадлежит к экспоненциальному семейству и невозможно найти оценку $\psi $, для которой достигается нижняя граница Рао-Крамера)?
Вопрос в том, как оценить необходимый объём выборки, чтобы можно было на практике подменять мат. ожидание выборочным средним?

Первое, что мне пришло в голову - посмотреть распределение выборочного среднего.
Но так как (даже при условии независимости отдельным реализаций) с такой ПРВ считать многомерные свёртки как-то кисло :(.
Я попытался воспользоваться ЗБЧ, а точнее теоремой Берри-Эссеена.
Тем самым я хотел оценить объём выборки, при котором распределение выборочного среднего будет отличаться от стандартного нормального распределения не более чем на заданную величину (например $0,001$). А тем самым в дальнейшем подменять распределение выборочного среднего нормальным распределением с соответствующими дисперсией и мат.ожиданием.

Оценка получилась следующая:
$\left|P\left(\frac{m^*-E(x)}{\sqrt{\frac{D[x]}{N_{\text{stat}}}}}<x\right)-\Phi _{0,1}(x)\right|\leq\frac{C E\left(|x-E(x)|^3\right)}{\sqrt{N_{\text{stat}}D[x]^3}}$,
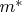
где $m^*$ - выборочное среднее.
Так как найти абсолютный центральный момент третьего порядка я не смог, то я произвёл оценку сверху (исходя из неравенства Гёльдера для вероятностных пространств). Получилось, что третий абсолютный момент не больше чем произведение корней из дисперсии и четвёртого центрального момента.
Т.е.
$\left|P\left(\frac{m^*-E(x)}{\sqrt{\frac{D[x]}{N_{\text{stat}}}}}<x\right)-\Phi _{0,1}(x)\right|\leq \frac{C \sqrt{E\left((x-E(x))^4\right)}}{\sqrt{N_{\text{stat}} D[x]^2}}$

Основная проблема в следующем:
Второй, третий и четвёртый моменты по $a$ имеют порядок $a^{-2}$. А это означает, что правая часть растёт как $a$ (что на практике хорошо, т.к. его смысл - отношение мощности сигнала к шуму). Но если исходить из заранее заданной ошибки отклонения функций распределения необходимо какой-то просто астрономический объём выборки $N_{stat}$. Это сильно напрягает.
С точки зрения логики, вроде бы понятно, что дисперсия стремится к нулю и "гауссовина" переходит в дельта-функцию (т.е. вклад шума как бы нивелируется).
С другой стороны я могу (имею ли право?) ещё больше загрубить оценку и вместо корня из дисперсии в числителе поставить просто дисперсию, тогда скорость роста по $a$ в числителе и знаменателе будет примерно одинакова. А могу ещё загрубить и тогда правая часть будет вообще спадать по $a$и мне будет достаточно малого объёма выборки (чуть ли не десятка, супротив десятков миллионов в первом случае). Но это же жонглёрство и с точки зрения практики выглядит как-то неправильно...
Но практически-то что делать? Как оценить объём выборки, что бы при такой ПРВ выборочное среднее было адекватной оценкой мат.ожидания?

[_hum_]

Путанно все написано. Какая задача все-таки перед Вами стоит:
укажите, какое параметрическое семейство распределений рассматриваете ( $\{w(x; a,\psi)\}_{a,\psi}$ - ?), какие параметры в нем оцениваете ($\psi $- ?) и какую оценку этих параметров в явном виде предлагаете ($\Hat{\psi}(X) = ?$).