Joker_vDОчень хорошо вы сформулировали, спасибо.
Я не сторонник Эвереттовской интерпретации в буквальном смысле, но предпочитаю думать о поле как о континууме "теневых" частиц - это очень наглядно.
Я не знаю, что в этом наглядного, но самое главное, не думаю, что в этом вообще есть что-то правильное. Что такое "континуум частиц"?
Я предпочитаю думать о поле разными методами, но (почти) всегда - такими достаточно прозрачными, как волновые функции в каких-то координатах, или амплитуды каких-то состояний.
А если электрон один во вселенной (ну, сильно удален ото всего остального), куда переноситься энергия?
А никуда. Виртуальные фотоны отлетают от него на небольшое расстояние, но никуда не прилетают. В результате, актов взаимодействия нет.
Можете рассматривать обмен виртуальным фотоном между двумя электронами как туннельный эффект: фотон "сидит" в одном электроне, "хочет" в другой, но между ними - "барьер". Фотон "проходит под барьером", и оказывается в точке назначения. Этот образ (между прочим, математически точный) помогает понять свойства такого обмена: что будет, если второго электрона нет (барьер удлиняется до бесконечности), есть ли на самом деле фотон в "запрещённых" точках пространства (есть, так же как и ненулевая плотность вероятности частицы в области барьера в случае туннельного перехода), и так далее.
И виртуальные частицы можно все таки позаимствовать у вакуума только "на короткое время", а электростатическое поле неограниченно в пространстве.
Не надо думать про "заимствовать у вакуума". Если вы рассуждаете в терминах диаграмм Фейнмана, то у вас все виртуальные частицы выходят из реальных или из других виртуальных.
Насчёт неограниченности - это смотрите формулы (выше я слегка накосячил, но сейчас исправлюсь). Электростатическое поле - решение уравнения Лапласа

Базисная система решений - это произведения вида "по одной координате экспонента, по другой - синусоида". Такие решения действительно имеют место, в каком-нибудь прямоугольном резонаторе. Если мы рассматриваем поле точечной частицы, то оно раскладывается по этой базисной системе решений в интеграл Фурье, и в итоге получается потенциал Кулона

Здесь экспоненциального спадания уже нет, оно "спряталось". Поэтому говорят, что "электростатическое взаимодействие дальнодействующее". Хотя образовано оно виртуальными фотонами.
Теперь рассмотрим поле, образованное другими виртуальными частицами, массивными. Например, такими частицами (не в модельном, а в реальном случае) могут быть мезоны в ядерном взаимодействии, или векторные бозоны в слабом взаимодействии. Опуская лишние детали, в статическом случае это поле - решение уравнения

. Базисная система решений этого уравнения выглядит очень похоже: "по одной координате экспонента, по другой - синусоида", только формулы, связывающие между собой расстояния спадания экспонент и длины волн синусоид - другие (эти формулы называются дисперсионным соотношением). И вот, когда решение этого уравнения приспосабливается к точечному источнику, в итоге получается уже существенно другой результат: потенциал Юкавы

Из-за экспоненты, которая в данном случае осталась, если глядеть в достаточно большом масштабе, этот потенциал спадает очень быстро, от него практически ничего не остаётся. Про такие взаимодействия говорят, что они "короткодействующие". Величина

- это, по сути, масса частицы-переносчика, переведённая в характерную длину через множители скорость света и постоянную Планка. Так что соответствующие расстояния получаются очень маленькими (для электрона - порядка межатомного расстояния

для мезона - порядка межнуклонного расстояния

для слабого векторного бозона - ещё меньше, порядка

), и с этим связано, что ядерные и слабые взаимодействия были открыты только как квантовые, в квантовую эпоху.
И насчёт времени. Когда мы рассматриваем статическое поле, мы фиксируем

а это значит вовсе не то, что виртуальная частица существует "только короткое время". Ровно наоборот, предельный переход к этому случаю означает, что частица существует
всегда, и всегда неизменная. Вот когда мы добавляем реалистичности, и заряды начинают медленно двигаться, тогда у нас и частицы приобретают малую
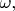
и могут существовать ограниченное время, не меньше чем

(потому что волновой пакет не может быть короче, чем самая короткая длина волны из тех, которые составляют этот пакет).