Помогите, пожалуйста, понять условие задачи (сумма n кубов)

[Xenia1996]

Доказать, что для каждого натурального n и каждого целого неотрицательного m уравнение

$x_1^3+x_2^3+\dots+x_n^3=y^{3m+2}$

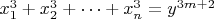
имеет бесконечно много решений в натуральных числах.

Я не поняла одну деталь в условии. Подразумевается ли, что $x_1, x_2, \dots, x_n$ обязаны быть попарно различными?
Если нет, то решение уж чересчур очевидно.

(Вот оно)

Если $x_i=n^k$, где k - натуральное, то $x_1^3+x_2^3+\dots+x_n^3=n^{3k+1}$, а поскольку среди чисел 3k+1 имеется бесконечно много делящихся на 3m+2, мы получаем бесконечно много решений.
Пример для n=17, m=2:


$(17^5)^3+(17^5)^3+\dots+(17^5)^3=17^{16}=(17^2)^8$

$(17^{13})^3+(17^{13})^3+\dots+(17^{13})^3=17^{40}=(17^5)^8$

$(17^{21})^3+(17^{21})^3+\dots+(17^{21})^3=17^{64}=(17^8)^8$

Ну и так далее.

Значит, я так понимаю, всё-таки иксы попарно различными быть должны?

[Null]

У вас в тексте ни где различность $x_i$ не требуется.