Derinaiborory писал(а):
я вычитаю не из прямоугольтника прямоугольник а из прямоугольника вычитаю половину, которая ограничена прямой и 1/n площади прямоугольника
Я этот метод понял и начал с проверки: а верно ли, что площадь между

и нижней стороной прямоугольника всегда составляет

его площади. До площади под
прямой я не дошел (и не дойду). Пожалуйста, просмотрите еще раз -- я анализирую ещё самый первый этап.
Если Вам понятнее в цифрах.
Берем кривую

, точки

и

. Площадь под кривой равна

-- это

Вашего прямоугольника
![$[0,2]\times[0^6, 2^6]$ $[0,2]\times[0^6, 2^6]$](https://dxdy-02.korotkov.co.uk/f/1/a/6/1a6585bf43f683e2b104e106a9a849aa82.png)
.
Берем кривую

, точки

и
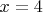
. Площадь под кривой равна

-- это тоже

Вашего прямоугольника
![$[0,4]\times[0^6, 4^6]$ $[0,4]\times[0^6, 4^6]$](https://dxdy-04.korotkov.co.uk/f/3/1/0/310d59de425a1056df92ea71857a775782.png)
.
Берем кривую

, точки

и
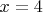
. Площадь под кривой равна разности двух предыдущих площадей

, согласны?
На интервале
![$x \in [2,4]$ $x \in [2,4]$](https://dxdy-01.korotkov.co.uk/f/8/e/5/8e57894a9073bbfa2dcebfc06962fe8982.png)
площадь между кривой

и горизонтальной линией

равна

, согласны?
Ну и равно ли это

от прямоугольника
![$[2,4]\times[2^6, 4^6]$ $[2,4]\times[2^6, 4^6]$](https://dxdy-01.korotkov.co.uk/f/0/5/4/0540643febd24b0024d7c91f9f55b18382.png)
?
Tlalok писал(а):
svv хочет сказать, что указанное Вами соотношение справедливо, ТОЛЬКО в том случае, если одна из точек

.
Именно!
