Дана последовательность случайных независимых чисел длинной m, распределенных равномерно на промежутке от 0 до base-1.

![$A_i\in[0,base-1], i=\overline{0,m-1}.$ $A_i\in[0,base-1], i=\overline{0,m-1}.$](https://dxdy-04.korotkov.co.uk/f/b/b/a/bba4b679dc64574b0451fe52006fe76182.png)
Событие

состоит в том, что

.
А событие
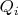
состоит в том, что

.
Введем понятие цепочки длиной

. Если в члене

происходит событие

, то считать это началом цепочки

. Длина цепочки будет определяться в зависимости от значения членов, стоящих правее члена

. Итак, если происходит событие

, то цепочка продолжается, иначе цепочка заканчивается. Если цепочка достигает конца ряда, то она тоже заканчивается.
Например:
если

, то

,
если

, то

,
если

, то

,
...
и т.д.
Пусть

.
Необходимо определить мат. ожидание (или хотя бы дать оценку сверху) для

.

.
Помогите пожалуйста. Подсказка, к какой теме относится данная задача, тоже будет не лишней.