
Если по каким то причинам эффективность очень важна (а иначе, и впрямь, лучше сортировать), воспользуйтесь известной задачей о «голандском флаге». Она является поворяющимся шагом быстрой сортировки (qsort, quicksort). Для любого значения

за один проход сегмента массива его можно реорганизовать на зоны

,
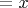
и

.
Идея проста: выбираем произвольное значение. Делим массив на три зоны. Каждый из наших индексов

попадает в одну из зон. Те, что попали в среднюю — найдены. Если в зоне нет ни одного индекса — забываем про нее. Иначе применяем к ней (и к попадающем в нее индексам) этот же процесс.
В среднем этот алгоритм дает линейное время, но при неудаче — квадратичное. На практике неудачи можно регулировать управляя выбором

. Кроме того, маленькие сегменты (меньше 10-15) может быть выгоднее отсортировать полностью каким нибудь пузырьком. Это уж надо на конкретной реализации выяснять.