Изменение знака ковариации

[darkhangelsky]

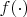
Дано:$\xi$ и $\eta$ - две неотрицательные случайные величины (одномерные); $cov(\xi,\eta)\ge0$. Пусть $f(\cdot)$ - убывающая неотрицательная функция (следовательно, $cov(\xi,f(\xi))\le0$). Верно ли, что $cov(\eta,f(\xi))\le0$? Иначе говоря, верно ли, что при убывающем преобразовании одной из случайных величин, ковариация меняет знак?

[--mS--]

Контрпример: возьмём таблицу совместного распределения
\begin{tabular}{l|c|c|c||c} \qquad$\xi$ & 0 & 1 & 2 & $\mathsf P(\eta=y_j)$ \cr $\eta$ \qquad & & & & \cr \hline \vphantom{\dfrac12}0 & 0 & $\frac12$ & 0 & $\frac12$ \\[1ex] \vphantom{\dfrac12}1 & $\frac14$ & 0 & $\frac14$ & $\frac12$ \\[1ex] \hline\hline \vphantom{\dfrac12}$\mathsf P(\xi=x_i)$ & $\frac14$ & $\frac12$ & $\frac14$ & 1 \cr \end{tabular}
Тогда $\mathsf E\xi=1$, $\mathsf E\eta = \frac12$, $\textrm{cov}(\xi, \eta) = 0$,

$$\textrm{cov}(\eta, f(\xi)) = \frac14 f(0)+\frac14 f(2) - \frac12\, \cdot\, \left(\frac14 f(0)+\frac12 f(1) + \frac14 f(2) \right) = \frac18\,\cdot\, \left(f(0)-2f(1)+f(2)\right).$$

Последнее выражение подбором убывающей $f$ может быть сделано любого знака. Например, положительно при $f(0)=3$, $f(1)=1$, $f(2)=0$.

[darkhangelsky]

Спасибо большое!