Convergence and divergence of series

[CrypticMath]

Hello,

I'm not sure of my answers to the following questions. Could someone check them, please?

$1.)\ \rm{Show\ that\ a\ geometric\ series\ \{a, ar, ar^2, ar^3,...\} is\ convergent\ if\ |r| < 1.}$

$\{a,\ ar,\ ar^2,\ ar^3,...\}$

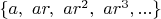
Now $\displaystyle S_n = \frac{a(1 - r^n)}{1 - r}$

and if $|r| < 1, \rm{then} \displaystyle \lim_{n\to \infty} r^n = 0$

So $\displaystyle\lim_{n\to \infty} S_n= \displaystyle\lim_{n\to \infty} \left[\frac{a(1 - r^n)}{1 - r}\right] = \frac{a}{1 - r}$

If $|r| > 1, \displaystyle \lim_{n\to \infty} r^n = \infty$ and the series does not converge.

Therefore, provided that $|r| < 1$, a Geometric Series converges to a sum of $\displaystyle \frac{a}{1 - r}$.


$2.)\ \rm{Show\ that\ all\ arithmetic\ series\ are\ divergent.}$

$\displaystyle S_n = \frac{n}{2}(2a + \overbrace{n - 1}.d)$

$\therefore$ with finite values for a and d, as $n$ increases, so does the value of $S_n$.

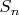
$\therefore$ if $n \rightarrow \infty$, then $S_n \rightarrow \infty$ in a positive or negative sense depending on the series.

[Sonic86]

Да вроде правильно...

[myra_panama]

по моему первая задача все решино , что еше доказать..???

[Joker_vD]

Well, everithing's right.

(Оффтоп)

Впервые увидел, как кто-то использует $\therefore$. Мы обычно $\Rightarrow$ пишем.

[CrypticMath]

спасибо!