Непрерывность

[Gortaur]

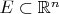
Пусть $A$ - компактное подмножество $E\subset \mathbb{R}^n$. Пусть также $K(x,dy)$ - ядро такое, что $K(x,E) = 1$ для всех $x\in E$. Пусть задана произвольная непрерывная на $A$ функция $u(x)$. Какие бы условия наложить на $K$ чтобы

$$ v(x) = \int\limits_A u(y)K(x,dy) $$

было также непрерывным на $A$? Что посоветуете? Непрерывность $K(x,B)$ для каждого борелевского $B$ вроде подходит, но слишком консервативно. Можно использовать непрерывность $K(x,C)$ для всех открытых $C$ или этого недостаточно?