Даны две противоположные вершины квадрата, лежащего в плоскости, проходящей через начало координат. Составить уравнение диагоналей и сторон квадрата. А(1,0,7). С(3,4,1)
Координаты третьей вершины равны

Эта вершина находится на одинаковом и известном расстоянии от вершин

и
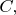
т.е. имеются два уравнения для двух неизвестных

и

которые легко решите.