I cannot use that function. Can you tell me the result. The problem have an application in geometry it is the reason to post it. I'll be very happy to know if there is some dependency between the variables. The problem I'm trying to solve is a "Sangaku" style problem. It is the statement:
It is given a circimscribed quadrilateral ABCD. Do there exist a dependency between
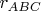
,
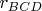
,
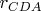
,
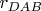
? What if we include

?
Here
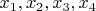
and

are the radii of the incircles mentioned and a,b,c,d are the respective tangents.

and

are the diagonals. I managed to get these equations but I failed on algebra.