Вопрос по логарифмическому отношению функций правдоподобия

[lomaxe]

Здравсвуйте!
Перед тем, как задать вопрос, немного теории из книги "Digital communications" by Bernard Sklar, потому что вопрос несколько связан с цифровыми коммуникациями.
В общем, допустим, существует коммуникационная система, где набор сигналов, передаваемых по каналу связи составляют$d=0,1$. Пускай, допустим, логическому нулю соответсвует значение напряжения -1В, а логической единице напряжение +1В.
В канале действует аддитивный белый гаусовский шум. Вероятность того, какой сигнал принят (логический нуль или логическая единица) обычно определяется по графикам функций правдоподобия для нуля и единицы, которые выглядят следующим образом:

$$p(x/d=-1)=\frac{1}{\sigma\sqrt{2\pi}}\exp\left\lbrack-\frac{1}{2}\left(\frac{x+1}{\sigma}\right)^2\right\rbrack$$

$$p(x/d=+1)=\frac{1}{\sigma\sqrt{2\pi}}\exp\left\lbrack-\frac{1}{2}\left(\frac{x-1}{\sigma}\right)^2\right\rbrack$$

$\sigma$ - среднеквадратическое отклонение белого шума.
Где х - уровень принятого сигнала. Подставляя в формулу х, определяем условные вероятности принятого сигнала. Условная вероятность которого сигнала больше, соответственно тот сигнал декодер и выдаёт на своём выходе.
Это, как бы является основой для принятия декодером решений, какой же сигнал всё-таки он получил.
Однако есть в теории цифровых коммуникаций такой алгоритм, как MAP (maximum a posteriori)
Суть его заключается в следующем:
при $p(d=1/x)>p(d=-1/x)$ принимается решение, что принята 1,
при $p(d=1/x)<p(d=-1/x)$ принимается решение, что принят 0.
И используетя так же теорема Байеса:

$$p(d=i/x)=\frac{p(x/d=i)P(d=i)}{p(x)}; i=0,1$$

и

$$p(x)=\sum_{i=0}^{1} p(x/d=i)P(d=i)$$

$p(x/d=i)$ - функция распределения вероятностей принимаемого сигнала х (с шумом)
$P(d=i/x)$ - апостериорная вероятность
$p(d=i)$ - априорная вероятность
$p(x)$ - функция распределения вероятностей принятого сигнала х, дающая тестовую статистику в пространстве сигналов 0 и 1.

Учитывая теорему Байеса и алгоритм MAP можно записать:
при $p(x/d=+1)P(d=+1)>p(x/d=-1)P(d=-1)$ принимается решение, что принята 1
при $p(x/d=+1)P(d=+1)<p(x/d=-1)P(d=-1)$ принимается решение, что принят 0

или

$$\frac{p(x/d=+1)P(d=+1)}{p(x/d=-1)P(d=-1)}>1$$

принимается решение, что принята 1

$$\frac{p(x/d=+1)P(d=+1)}{p(x/d=-1)P(d=-1)}<1$$

принимается решение, что принят 0

Если взять натуральный логарифм, то мы получим полезную метрику, называемую LLR(log-liklyhood ratio):

$$L(d/x)=log_e\left[\frac{p(x/d=+1)}{p(x/d=-1)}\right]+log_e\left[\frac{P(d=+1)}{P(d=-1)}\right]$$

Или же в конечном итоге можно записать:

$$L(\widehat{d})=L_c(x)+L(d)$$

где $L_c(x)=log_e\left[\frac{p(x/d=+1)}{p(x/d=-1)}\right]$ - LLR тестовой статистики х, получаемой путём измерений х на выходе канала при чередовании условий, что может быть передан d=+1 или d=-1.
$L(d)=log_e\left[\frac{P(d=+1)}{P(d=-1)}\right]$ - априорное LLR бита данных d.
Для систематических корректирующих кодов доказано, что LLR на выходе декодера равно:

$$L(\widehat{d})=L_c(x)+L(d)+L_c(\widehat{d})$$

Тут $L_c(x)+L(d)$ - это LLR, полученное из демодулятора, т.е. значение, получаемое из знания априорной вероятности битов и условной вероятности.

$L_c(\widehat{d})$ - называется внешним LLR и представляющую внешнюю информацию, вытекающего из декодирования. Она вытекает из того, что в полезное сообщение добавляются добавочные биты, способные дать нам дополнительные знания о том, насколько верно принята последовательность данных.
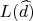
Как результат, $L(\widehat{d})$ при положительном значенни говорит нам, что получена логическая единица, при отрицательном - логический нуль.
При вычислении внешней информации используется LLR алгебра:

$$L(d_1)\boxplus L(d_2 )\triangleq L(d_1\oplus d_2)=log_e \left[\frac{e^{L(d_1)}+e^{L(d_2)}}{1+e^{L(d_1)}e^{L(d_2)}}\right]$$

Знак $\boxplus$ представляет LLR сложение, а знак $\oplus$ представляет сложение по модулю 2.

Привожу ниже доказательсво этого выражения (это важно для сути вопроса):

$$L(d)=log_e \left[\frac{P(d=+1)}{P(d=-1)}\right]=log_e \left[\frac{P(d=+1)}{1-P(d=+1)\right]}$$

отсюда:

$$e^{L(d)}=\left[\frac{P(d=+1)}{1-P(d=+1)}\right]$$

Решая относительно P(d=+1), получаем:

$$e^{L(d)} - e^{L(d)}\times P(d=+1)=P(d=+1)$$

$$e^{L(d)}=P(d=+1)\times [1+e^{L(d)}]$$

и

$$P(d=+1) =\frac{e^{L(d)}}{1+e^{L(d)}}$$

$$P(d=-1)=1-P(d=+1)=1-\frac{e^{L(d)}}{1+e^{L(d)}}=\frac{1}{1+e^{L(d)}}$$

$$L(d_1 \oplus d_2)=log_e \left[\frac{P(d_1 \oplus d_1=1)}{P(d_1 \oplus d_1=-1)}\right]$$

$$=log_e\left[\frac{P(d_1=+1)\times P(d_2=-1)+[1-P(d_1=+1)][1-P(d_2=-1)]}{P(d_1=+1)\times P(d_2=+1)+[1-P(d_1=+1)][1-P(d_2=+1)]}\right]$$

Ну и подставляя в это выражение

$$P(d=+1) =\frac{e^{L(d)}}{1+e^{L(d)}}$$

и

$$P(d=-1)=\frac{1}{1+e^{L(d)}}$$

Получаем

$$L(d_1)\boxplus L(d_2 )=log_e \left[\frac{e^{L(d_1)}+e^{L(d_2)}}{1+e^{L(d_1)}e^{L(d_2)}}\right]$$

А теперь, как это всё получается практически (и там то и возникнет самый главный вопрос, который касается большей частью математики и ради которой я создал эту тему):
Пускай передаются данные, представленные в таблице:

$$\begin{tabular}{|l|l|l|}\hline d_1=1 & d_2=0 & p_{12}=1\\ \hline d_3=0 & d_4=1 & p_{34}=1\\ \hline p_{13}=1 & p_{24}=1&\\ \hline \end{tabular}$$

Тут $d_1,d_2,d_3,d_4$ это полезные данные, а $p_{12},p_{34},p_{13},p_{24}$ - это проверочные биты, полученные путём сложения полезных данных по формуле, как показано ниже:

$$d_i \oplus d_j=p_{ij}$$

Данные передаются в такой последовательности:

$$d_1,d_2,d_3,d_4,p_{12},p_{34},p_{13},p_{24}$$

и соответственно переданная последовательность будет выглядеть:

$$\{d_i\},\{d_{ij}\}=1\ 0\ 0\ 1\ 1\ 1\ 1\ 1$$

Если информационные биты выразить через значения биполярного электрического напряжения +1 и -1, соответствующие логическим двоичным уровням 1 и 0, то представленная последовательность будет следующей:

$$\{d_i\},\{d_{ij}\}=+1,-1,-1,+1,+1,+1,+1,+1$$

На входе приёмника повреждённые шумом биты обозначим последовательностью $\{x_i\},\{x_{ij}\}$ где $x_i=d_i+n$ для каждого принятого бита данных, $x_{ij}=p_{ij}+n$ для каждого полученного проверочного бита, а n представляет собой распределение помех, которое статистически независимо для $x_i$ и $p_{ij}$
Предположим, что вследствии воздействия помех, на вход приёмника приходит последовательность:

$$\{x_i\},\{x_{ij}\}=0,75,\ 0,05,\ 0,10,\ 0,15,\ 1,25,\ 1,0,\ 3,0,\ \ 0,5$$

или другими словами мы принятую последовательность можем записать:

$$\{x_i\},\{x_{ij}\}=x_1,x_2,x_3,x_4,x_{12},x_{34},x_{13},x_{24}$$

$L_c(x_k)$ найдём по формуле(здесь $k$ в обозначении $x_k$ является общим временным индексом k=1,2,3,4,5,6,7,8):

$$L_c(x_k)=log_e \left[\frac{p(x_k/d_k=+1}{p(x_k/d_k=-1}\right]=log_e \left (\frac{\frac{1}{\sigma\sqrt{2\pi}}\exp\left\lbrack-\frac{1}{2}\left(\frac{x_k-1}{\sigma}\right)^2\right\rbrack}{\frac{1}{\sigma\sqrt{2\pi}}\exp\left\lbrack-\frac{1}{2}\left(\frac{x_k+1}{\sigma}\right)^2\right\rbrack}\right)=- \frac{1}{2} {\left (\frac{x_k-1}{\sigma}}\right)}^2+\frac{1}{2} {\left (\frac{x_k+1}{\sigma}}\right)}^2=\frac{2}{{\sigma}^2}x_k$$

И делая допущение, что ${\sigma}^2=1$

$$L_c(x_k)=2x_k$$

Вычисленные значения $L_c(x_k)$ для каждого из принятых бит данных запишем в таблицу:

$$\begin{tabular}{|l|l|l|}\hline L_c(x_1)=1,5 & L_c(x_2)=0,1 & L_c(x_{12})=2,5 \\ \hline L_c(x_3)=0,2 & L_c(x_4)=0,3 & L_c(x_{34})=2,0\\ \hline L_c(x_{13})=6,0 & L_c(x_{24})=1,0 &\\ \hline \end{tabular}$$

По сути, на основе этих данных в таблице, мы могли бы определить значения принятых бит, но мы можем увидеть, что в таком случае мы сделаем две ошибки в вычислении принятых битов. Шум настолько исказил данные, что декодер просто допустит ошибки в вычислении значений бит.
Однако, мы можем вычислить внешний LLR пользуясь тем, что мы вводили проверочные биты p. И используя внешний LLR уточнять LLR данных в общем.
Делаем это мы следующим образом(например, для $d_1$):

$$L(\widehat{d_1})=L_c(x_1)+L(d_1)+\{[L_c(x_2)+L(d_2)] \boxplus L_c(x_{12})\}$$

Выражение
$[L_c(x_2)+L(d_2)] \boxplus L_c(x_{12})$ является нашим внешним LLR, вычисленным из знания значения проверочного бита по горизонтали. То же самое можно сделать и по вертикали:

$$L(\widehat{d_1})=L_c(x_1)+L(d_1)+\{[L_c(x_3)+L(d_3)] \boxplus L_c(x_{13})\}$$

В общем случае, уточнённое значение бита полезных данных будет выражаться как:

$$L(\widehat{d})=L_c(x)+L_{eh}(\widehat{d})+L_{eh}(\widehat{d})$$

где $L_{eh}(\widehat{d})$ - внешний LLR, полученный путём горизонтального декодирования
а $L_{ev}(\widehat{d})$ - внешний LLR, полученный путём вертикального декодирования.
Сделаем необходимые вычисления, учитывая, что $L(d)$ для первого прохода будет равен нулю, так как мы предполагаем, что от источника вероятность появления 0 и 1 равны:

$$L_{eh}(\widehat{d_1})=[L_c(x_2)+L(d_2)] \boxplus L_c(x_{12})=(0,1+0) \boxplus 2,5 \approx -0,1 = $новое значение$\ L(d_1) $$

$$L_{eh}(\widehat{d_2})=[L_c(x_1)+L(d_1)] \boxplus L_c(x_{12})=(1,5+0) \boxplus 2,5 \approx -1,5 = $новое значение$\ L(d_2) $$

$$L_{eh}(\widehat{d_3})=[L_c(x_4)+L(d_4)] \boxplus L_c(x_{34})=(0,3+0) \boxplus 2,0 \approx -0,3 = $новое значение$\ L(d_3) $$

$$L_{eh}(\widehat{d_4})=[L_c(x_3)+L(d_3)] \boxplus L_c(x_{34})=(0,2+0) \boxplus 2,0 \approx -0,2 = $новое значение$\ L(d_4) $$

Теперь то же самое декодирование делаем по вертикали, с той лишь разницей, что мы уже имеем уточнённые LLR $L(d)$ из горизонтального декодирования:

$$L_{ev}(\widehat{d_1})=[L_c(x_3)+L(d_3)] \boxplus L_c(x_{13})=(0,2-0,3) \boxplus 6,0 \approx 0,1 = $новое значение$\ L(d_1) $$

$$L_{ev}(\widehat{d_2})=[L_c(x_4)+L(d_4)] \boxplus L_c(x_{24})=(0,3-0,2) \boxplus 1,0 \approx -0,1 = $новое значение$\ L(d_2) $$

$$L_{ev}(\widehat{d_3})=[L_c(x_1)+L(d_1)] \boxplus L_c(x_{13})=(1,5-0,1) \boxplus 6,0 \approx -1,4 = $новое значение$\ L(d_3) $$

$$L_{ev}(\widehat{d_4})=[L_c(x_2)+L(d_2)] \boxplus L_c(x_{24})=(0,1-1,5) \boxplus 1,0 \approx 1,0 = $новое значение$\ L(d_4) $$

Теперь, используя формулу

$$L(\widehat{d})=L_c(x)+L_{eh}(\widehat{d})+L_{eh}(\widehat{d})$$

и значения внишних LLR при горизонтальном и вертикальном деокдировании для соответствующих битов, мы можем найти уточнённые значения полученных данных и записать их в таблицу:

$$\begin{tabular}{|l|l|l|}\hline L_c(x_1)=1,5 & L_c(x_2)=-1,5 & L_c(x_{12})=2,5 \\ \hline L_c(x_3)=-1,5 & L_c(x_4)=1,1 & L_c(x_{34})=2,0\\ \hline L_c(x_{13})=6,0 & L_c(x_{24})=1,0 &\\ \hline \end{tabular}$$

Как мы видим, внешние LLR сыграли хорошую роль в том, чтобы уточнить LLR полезных данных.
А теперь вопрос, который у меня возник при всех этих вычислениях.
При выводе формулы

$$L(d_1)\boxplus L(d_2 )=log_e \left[\frac{e^{L(d_1)}+e^{L(d_2)}}{1+e^{L(d_1)}e^{L(d_2)}}\right]$$

Мы использовали, как бы это правильно сказать, дискретное значение вероятности. Т.е., мы знали, что если у нас есть значение $P(d=+1)$, то мы можем найти значение $P(d=-1)=1-P(d+1)$
Но при вычислениях внешних LLR, используя логарифмическое сложение со знаком $\boxplus$ мы применяли это по отношению к условным значениям вероятностей $p(x/d=+1)$ или $p(x/d=-1)$. Вот у меня и зародился вопрос - а насколько это справедливо? Можно ли применять формулу, которая была выведена на основе неусловных вероятностей к функции распределения вероятностей. Может ли такое быть, что $p(x/d=+1)=1-p(x/d=-1)$?
Собственно, в этом и вопрос. Извиняюсь, конечно, что пришлось выложить столько теории, но это для того, чтобы вопрос был более понятным.

-- Чт янв 06, 2011 22:51:55 --

Кстати, всех с рождеством Христовым :)