абсолютная непрерывность

[RIP]

Всё-таки решил спросить. Можно ли как-то по-простому доказать, что если $f\colon[a,b]\to\mathbb R$ --- дифференцируемая функция ограниченной вариации, то $f$ абсолютно непрерывна?

[Gortaur]

Глупый вопрос можно? А зачем Вам ограниченность вариации как дополнительной свойство? Она разве не следует из дифференцируемости и компактности?

[RIP]

Не следует. Функция $f(x)=x^2\sin x^{-10}$ всюду дифференцируема, но не ограниченной вариации на $[0,1]$.

-- Вт 04.01.2011 13:45:05 --

Да, "по-простому" значит "с минимумом науки". Через науку утверждение доказывается в одну строчку.

[sup]

А что если представить её как разность двух монотонных непрерывных функций?

[RIP]

Во-первых, придётся помучиться, чтобы добиться их дифференцируемости (иначе какой смысл представлять?), а во-вторых, для монотонной функции это утверждение мне тоже не очевидно.

[sup]

Хм. Предлагается такой план. Сразу отмечу, дифференцируемость $f$ не нужна, достаточно непрерывности.
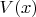
Положим $V(x),x \in [a,b]$ вариация $f$ на отрезке $[a,x]$. Далее, $U(x)=V(x)-f(x)$. Легко видеть, что $V(x), U(x)$ монотонны и их разность $V(x)-U(x)=f(x)$. Сначала доказываем, что $V(x)$ непрерывна. У меня имеется набросок доказательства от противного. Затем, докажем. что монотонная непрерывная на $[a,b]$ функция - абсолютно непрерывна. (Отсюда уже легко следует абс. непрерывность $f$). 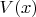Рассмотрим $V(x)$ и её "перестановки", которые определяются следующим образом. Пусть $x_1=a \leqslant x_2 \leqslant .... \leqslant x_n=b \in [a,b]$ . Переставим интервалы $[x_k,x_{k+1}]$ "вместе с графиком $f$" произвольным образом, а затем двигая куски графика вверх-вниз склеим в непрерывную функцию.
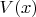
Все эти функции равномерно ограничены и равностепенно непрерывны. А вот теперь, действуя от противного, если $V(x)$ не является абс. непрерывной, то можно предъявить последовательность таких перестановок, которые все хуже и хуже устроены в точке $x=a$. По теореме Асколи-Арцела получаем противоречие.

-- Ср янв 05, 2011 00:12:19 --

Ой, выдал желаемое за действительное. Точно, есть над чем подумать.

[RIP]

sup в сообщении #395325 писал(а):

монотонная непрерывная на $[a,b]$ функция - абсолютно непрерывна

это неверно: стандартный контрпример --- лестница Кантора. Дифференцируемость (всюду, за исключением не более чем счётного множества) дело спасает, но вот как это увидеть непосредственно?