В 4.11. бред написал, не читайте там

. Вот так, наверное, правильно должно быть:
На всякий случай напишу все данные векторы:
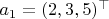
,

,

,

,

,

.
Если из определения матрицы лин. отображения (назовём её

) исходить, получим

, а это 3 СЛАУ:

Ещё две аналогичные СЛАУ и получаем

Я проверил:

даёт

и т. д, то есть матрица, похоже, составлена верно и базис тот же, в каком даны

и

. Но может как-то проще можно решить, без трёх системок?