Олимпиада "Обыкновенные дифференциальные уравнения", Мехмат МГУ, 2006
1. (1 балл) Одно из решений системы уравнений

устойчиво по Ляпунову. Докажите, что любое решение устойчиво по Ляпунову.
2. (2) Найдите производную порядка

по параметру

в
точке

выражения

, где

- произвольная обратимая матрица размерности

.
3. (2) Докажите, что у линейной системы

не может быть предельных циклов (изолированных периодических решений).
4. (5) Известно, что

- решение уравнения

,

, и что решение

его линеаризации

асимптотически устойчиво. Покажите на примере, что нулевое решение исходного уравнения может не быть асимптотически устойчивым.
5. Дифференциальное уравнение

,

с непрерывной правой частью не удовлетворяет в некоторых точках условиям теоремы о единственности решения. Может ли оно иметь:
a) (2 балла) множество решений

, для которых
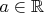
,

, и

?
б) (3 балла) два решения

, такие, что

,

, а

,

?
в) (2) такие же вопросы для уравнения вида

,

.
6. (3) Докажите, что для всякого ненулевого решения

уравнения

и любого

найдутся два различные момента времени

,

такие, что

и

.
7. (5) Докажите, что нулевое решение уравнения

асимптотически устойчиво, если известно, что

, и при

,

,

. (

,

- гладкие.)
8. (5) Решите систему уравнений

, с матрицей

.
9. а) (2) Пусть

и

- два линейно независимых решения линейного дифференциального уравнения третьего порядка. Может ли определитель Вронского

и

обращаться в 0 на некотором интервале?
б) (3) Пусть

и

- три линейно независимых решения линейного дифференциального уравнения четвертого порядка. Может ли определитель Вронского

и

обращаться в 0 на некотором интервале?
10. (3) Нарисуйте фазовый портрет системы

11. (4) Оцените отличие от

периода решения уравнения физического маятника

с малой амплитудой

.
12. (5) Правая часть дифференциального уравнения математического маятника с трением (и внешней силой):

является гладкой функцией, удовлетворяющей условию

,

,

- неотрицательное,

- положительное числа.
При каких значениях

,

,

можно так выбрать

, чтобы раскачать маятник, т.е. чтобы для некоторого решения
![$\sup\limits_{t\in[0,T]} |x(t)|\to\infty$ $\sup\limits_{t\in[0,T]} |x(t)|\to\infty$](https://dxdy-01.korotkov.co.uk/f/c/9/0/c902f28e7d0c3f4af38bd7d68048261482.png)
при

?