nnosipov писал(а):
Новый параметр

--- это, наверное, старый

?
Да, совершенно верно. Я этого не заметил, потому что получил свои формулы другим способом (который математики наверняка назовут нечестным

):
1. Написал программу на C++, которая в достаточно широком диапазоне перебирает

и

и находит пары, удовлетворяющие условию задачи.
2. Отобразил все найденные точки

на графике. Удобно использовать оси

,

.
3. Заметил, что все точки естественно разбиваются на "серии" -- ложатся на непересекающиеся кривые. Параметр

-- это как раз номер серии.
4. Зная координаты точек, для каждой из первых 5 серий вручную подобрал формулы
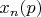
,

(

-- номер точки в серии). Оказалось, что
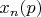
-- полином степени

от

,

-- полином степени

от

.
5. Заметил, что для полиномы для соседних

удовлетворяют рекуррентному соотношению

, та же формула для

.
6. По рекуррентной формуле нашел производящую функцию и затем получил явные выражения для
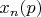
,

.
7. Воспользовался "принципом программистской индукции": если в рассматриваемой области все точки получаются из найденных формул, то и вообще все подходящие пары

получаются из этих формул.

nnosipov писал(а):
Буду рад, если поделитесь ощущениями.
Очень приятная и интересная задача. Хотя, как видите, я оценивал её совсем в другом ракурсе.