штрих Шеффера

[Xaositect]

Xaositect в сообщении #388267 писал(а):

Шефферова функция должна не лежать ни в одном из 5 предполных классов. Осталось оценить количество таких функций. Ну там самодвойственных и линейных мало, классы сохранения дают как раз четверть, а немонотонность следует из несохранения констант.

[CYHDYK]

Огромное спасибо за отличную книгу. На самом деле так и есть, это не кол-во штрихов шеффера, а как раз кол-во ф-ий шеффера размерности n.

[nandreao]

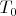
Нашел доказательство, что функция является шефферовой, если не является сохраняющей константу и самодвойственной, т.е. не принадлежит объединению множеств $T_{0}$ U $T_{1}$ U $S$. Соответственно число шефферовых функций равно разности мощности множества всех бул.функций и упомянутого объединения.
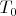
Нашел формулу $|P_{2}^n$ \ $T_{0}$ U $T_{1}$ U $S| = 2^{2^n-2} - 2^{2^{n-1}-1}$, но как доказать ее не знаю.
Понятно, что количество всех булевых функций $2^{2^n}$,
$|T_{0}| = |T_{1}| = 2^{2^n-1}$
А как оценить мощность S и получить упомянутую формулу?