Есть двумерная случайная величина

. Ее распределение таково: пусть
![$Q = [-1,1]^2$ $Q = [-1,1]^2$](https://dxdy-03.korotkov.co.uk/f/2/a/5/2a51d7469abe70219aa039d2655cc41682.png)
и
![$Q' = [\frac{1}{2},\frac{1}{2}]^2$ $Q' = [\frac{1}{2},\frac{1}{2}]^2$](https://dxdy-01.korotkov.co.uk/f/4/9/9/499af1b4024e060160c270488bc3769b82.png)
, кроме того

. Тогда

если

или

если

. Здесь

равномерно распределено в квадрате
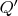
,

стандартно нормально распределено.
Получаем, что

. Требуется найти

- плотность распределения

. Имеем

То есть

Пусть теперь

, тогда

Если взять

, то

что по сути не обязано выполнять - в чем ошибка, почему противоречие получилось?
-- Чт дек 16, 2010 18:49:51 --Ошибку нашел: она в том, что

- и все отлично получается. Теперь другой вопрос, если

- двумерная нормальная величина, какая у нее плотность при условии что

?
-- Чт дек 16, 2010 18:53:03 --Ошибку нашел - запутался в условных вероятностях, вопрос снят.