Здравствуйте!
Читаю доказательство теоремы о равномощности бесконечного множества и его объединения с конечным или счетным множеством.
Формулировка:
«Если

— бесконечное множество, а

— конечно или счетно, то

равномощно

».
Теорема доказывается следующим образом:
Выберем в

счетное множество

и обозначим

как

. Тогда
![$\[M = B \cup A',M \cup A = B \cup A \cup A'\]$ $\[M = B \cup A',M \cup A = B \cup A \cup A'\]$](https://dxdy-03.korotkov.co.uk/f/e/0/d/e0dbd32182f44669e61c5d820a76550382.png)
. Множество
![$\[A \cup A'\]$ $\[A \cup A'\]$](https://dxdy-04.korotkov.co.uk/f/3/6/d/36d6d6108563e4e48d3b8e36b60d38b082.png)
счетно,

и
![$\[A \cup A'\]$ $\[A \cup A'\]$](https://dxdy-04.korotkov.co.uk/f/3/6/d/36d6d6108563e4e48d3b8e36b60d38b082.png)
равномощны, и существует биекция

. Рассмотрим отображение

, определяемое по закону:

Утверждается, что

— биекция. В процессе доказательства того, что это инъекция, утверждается: если

. Однако, я не совсем согласен с тем, что

. Представим себе следующее построение множества

и множества

:

— множество точек

на плоскости,

— точки на этом отрезке, точки

лежат на прямой, перпендикулярной лучу

.
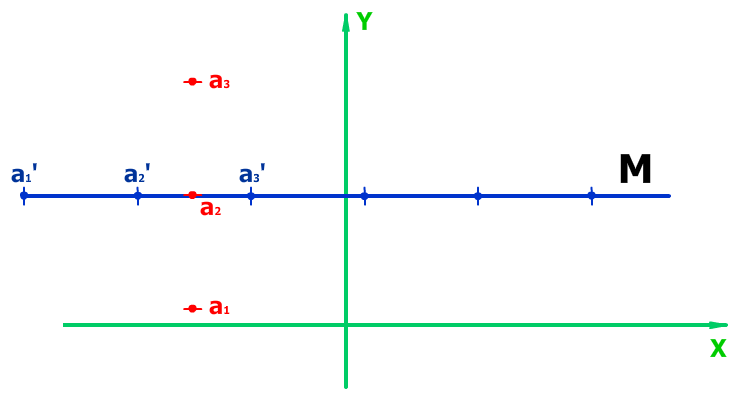
Пусть

строится следующим образом:

Пусть

То есть условие не выполняется.
На мой взгляд, можно проделать следующее, чтобы было более корректно: так как

конечно или счетно, то

также будет счетным или конечным. Пусть
![$\[\psi :A' \to (A'\; \cup \left( {A\backslash B} \right))\]$ $\[\psi :A' \to (A'\; \cup \left( {A\backslash B} \right))\]$](https://dxdy-01.korotkov.co.uk/f/4/4/2/4429a079b75fdf6a67f763fd8743243c82.png)
— биекция. В таком случае

как раз и будет требуемой биекцией.
Подскажите, пожалуйста, правильно ли я рассуждаю, что первоначальное доказательство не совсем корректно? Заранее спасибо :).