В дне цилиндрического сосуда радиусом

имеется круглое отверстие радиусом

. Найти зависимость скорости понижения уровня воды в сосуде от высоты этого уровня

. Жидкость идеальная.
Я решила так:

С другой стороны:

Приравниваем правые части:
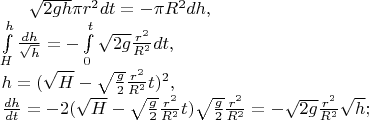
В итоге:

Скажите пожалуйста, верно ли решение и ответ ?