
1. Докажем, что

. Это равносильно

. Обозначим

,

. Тогда нужно доказать, что

.
Треугольник

равнобедренный (

), тогда

. Рассмотрим

: по теореме косинусов

. Подставляем в

:

, ч. т. д.
2. Докажем, что

.
Треугольник

равнобедренный (

),
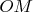
-- биссектриса (т. к.

по трём сторонам). Обозначим

. Тогда

. Значит

, ч. т. д.
Из 2) непосредственно следует

.