Проверьте пожалуйста правильно ли я нашел
Задание
Найти

, если

где

Вначале как я понял нужно выразить

Проверьте пожалуйста правильно ли я это сделал с x-ом

если нет то как правильно?Нужно ли так делать вообще?
И правильно ли я нашел

=

где
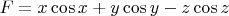
А потом надо это подставить в

так?
Просто у меня очень огромное выражение получается