Вот проблеме с исследованием задач на построение.Сами задачи я решил, т.е построение произвёл и доказательство с анализом тоже.
1.Построить треугольник по стороне прилежащему к к ней углу и сумме двух оставшихся сторон.
с построением проблем не возникло.Но вот сколько решений и при каких условиях задача имеет решения, тут возникли проблемы. Я думаю что решение единственное.Если обозначим известную сторону за

, а за сумму остальных двух сторон через

, то условие при котором задача будет иметь решение будет
![$ \[
a \leqslant d
\]$ $ \[
a \leqslant d
\]$](https://dxdy-01.korotkov.co.uk/f/4/c/9/4c9fdf1177fb170f6fea1cdb02039d9b82.png)
Почти правильно. Если "меньше либо равно" заменить на "меньше" будет совсем правильно. (Ну и угол, конечно, должен быть от

до

)
-- 02 ноя 2010, 02:50 --2
Построить треугольник по двум сторонам и медиане проведённой к одной из этих сторон. Опять же с построением проблем нет.Я получил что решение единственно.Вот какое здесь условие для сущ, решения нужно ???
Вы сначала строили треугольник, в котором сторонами являются медиана, половина стороны, на которую она опущена, и другая сторона, верно? А при каких условиях существует этот треугольник?
-- 02 ноя 2010, 03:16 --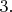
построить треугольник стороне прилежащему к ней углу и высоте опущенной на третью сторону. Опять же я построил, но решений два.А на сущ решения какие условия?
Здесь похитрее будет.
Пусть даны сторона

, угол

и высота
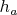
.
Одно необходимое условие существования решения довольно простое. Ясно, что высота не может быть больше прилежащей стороны. Т.е. должно выполняться

. При равенстве будет получаться единственное решение при условии, что угол

меньше прямого.
Если

строго больше
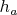
, то надо рассмотреть условия

и

. Условие существования треугольника - выполнение хотя бы одного из них. Если будут выполняться оба, то решений будет два.