Икс и игрек (задача с XXV всесоюзки)

[nnosipov]

Помещу-ка я на всякий случай доказательство сделанных мною выше утверждений (вдруг кому-нибудь захочется их как-то прокомментировать и/или дополнить).

1. Если числа $x$ и $y$ удовлетворяют условию задачи, то система уравнений Лича

$$ X^2+Y^2=Z^2, \quad X^2+z^2Y^2=W^2, $$

где $z=y-x>0$, разрешима в натуральных числах $X$, $Y$, $Z$, $W$. Действительно, если $z=kl$ ($k$, $l$ --- из моего решения), то можно взять

$$ X=\frac{l^2-k^2}{2}, \quad Y=\sqrt{(k^2+1)(l^2+1)}, \quad Z=\frac{k^2+l^2+2}{2}, \quad W=\frac{2k^2l^2+k^2+l^2}{2}. $$

Такие числа $z$ довольно редки; так, в пределах первой тысячи их имеется всего шесть: это $7$, $41$, $76$, $239$, $287$, $351$.

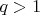2. Если числа $x$ и $y$ удовлетворяют условию задачи, то либо $\gcd{(x,y+1)}=1$, либо $\gcd{(y,x+1)}=1$. Заметим, что в первоначальном виде задача эквивалентна следующему предложению: если $p>1$ и $q>1$ --- натуральные числа, не являющиеся точными квадратами, то уравнения

$$ pu^2-qv^2=1, \quad qu^2-pv^2=1 $$

не могут быть одновременно разрешимыми. Легко видеть, что в теперешнем виде задача эквивалентна усиленной версии этого предложения --- без ограничения "не являющиеся точными квадратами". Ясно, что числа $p$ и $q$ не могут быть точными квадратами одновременно. Пусть теперь $p=r^2>1$, а $q$ точным квадратом не является. Мы хотим показать, что уравнения

$$ u^2-qv^2=1, \quad u^2-qv^2=-1 $$

не могут иметь таких решений $(U,V)$ и $(U^*,V^*)$ соответственно, что $U \equiv U^* \equiv 0 \pmod{r}$. Для этого рассмотрим минимальное решение $\xi$ второго из уравнений. Тогда

$$ U+V\sqrt{q}=\xi^s, \quad U^*+V^*\sqrt{q}=\xi^t, $$

где $s$ чётно, а $t$ нечётно. Положим $d=\gcd{(s,t)}=is+jt$, где $i$, $j$ --- некоторые целые числа. Нетрудно видеть, что если $\xi^d=U_d+V_d\sqrt{q}$, то

$$ 0 \equiv \begin{cases} V_d, & \text{если $i+j$ чётно},\\ U_d, & \text{если $i+j$ нечётно} \end{cases} \pmod{r}. $$

Однако $d=i_1s+j_1t$, где $i_1=i-t$, $j_1=j+s$ и поэтому числа $i_1+j_1$ и $i+j$ имеют разную чётность. Таким образом, $U_d \equiv V_d \equiv 0 \pmod{r}$, что невозможно.