решение параболического ур-ния с помощью интегральн. преобр.

[oposum]

Пусть надо решить параболическое уравнение

$$\frac{\partial C(t,r,\varphi)}{\partial t}=\frac{1}{r}\frac{\partial}{\partial r}\left(rK\frac{\partial}{\partial r}\right)C+\frac{1}{r^2}\frac{\partial^2}{\partial^2 \varphi}C+\frac{\partial^2}{\partial^2 z}C.$$

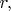
В книжке, которую я читаю, предложен следующий способ сделать это: избавимся сначала от дифференцирования по $r,$ приравнивания интегрального преобразование

$$\int\limits_{r_0}^{r_1}\left(\frac{\partial C}{\partial t}-\frac{1}{r}\frac{\partial C}{\partial r}\left(rK\frac{\partial}{\partial r}\right)-\frac{\partial^2C}{\partial^2 z}\right)W(r)rdr=0$$

с ядром $W(r)$ и весом $r$ к нулю. И дальше находят, что это ядро есть линейная комбинация функций Бесселя 1ого и 2ого рода. Потом с помощью синус-преобразования Фурье избавляются от $z,$ а затем делают обратные преобразования.
Вопрос: почему так можно делать?

[oposum]

Вообще не очень понятно, когда надо применять преобразование Фурье, а когда Ханкеля, и можно ли принять метод разделения переменных при решении уравнения в неограниченной области.

[ewert]

oposum в сообщении #366728 писал(а):

когда надо применять преобразование Фурье, а когда Ханкеля,

Без конкретной постановки граничных условий -- неизвестно.

oposum в сообщении #366728 писал(а):

можно ли принять метод разделения переменных при решении уравнения в неограниченной области

Нельзя (без дополнительных идеализаций) -- спектр не дискретен.

[oposum]

Уравнение рассматривается в области $r_0\leq r\leq r_1,\,0\leq\varphi\leq 2\pi,\,0\leq z<\infty,\,0<t<\theta.$
Граничные условия: $\left.C(t,r,\varphi,z)\right|_{r=r_0,r_1}=\left.C(t,r,\varphi,z)\right|_{z=0}=0,\:\left.C(t,r,\varphi,z)\right|_{z\to\infty}=0.$
Начальные условия:
$C(0,r,\varphi,z)=C(\theta,r,\varphi,z)$

[oposum]

так как в моем случае?

[moscwicz]

я бы применил преобразование Лапласа по z, а потом стал бы решать параболическое уравнение на изображение путем разложения по собственным функциям оператора Лапласа + что там получится

кстати, а вас $C= 0$ не устроит?

[oposum]

moscwicz, ну там еще в правой части исходного уравнения есть дельта-функция, поэтому у однородного хотелось бы найти нетривиальное решение..
по преобразованию Ханкеля-- на сколько я понимаю, оно применяется, когда есть некая осевая симметрия?