У них нет и не может быть плотности совместного распределения - ни относительно меры Лебега, ни относительно считающей меры. Совместное распределение пары
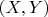
с данной функцией распределения сингулярно в

, поскольку сосредоточено на множестве нулевой лебеговой меры в

и не имеет атомов. Поэтому никаких интегралов ни от чего тут выписать не удастся. Впрочем, тут я не сильна.
Обратный факт следует просто из того, что функция распределения однозначно определяет распределение - хоть в

, хоть в

. Поэтому если пара

, где

имеет данную функцию распределения, и пара

имеет ту же функцию распределения, то совместное распределение пары

такое же, как у пары

. В частности,

для любого борелевского

. Например, для

, совпадающего с диагональю единичного квадрата.