Сеть Петри

[cyb12]

Есть такая сеть Петри:

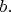
Утверждается, что она порождает контекстно-свободный язык $\{a^nb^n|n>1\}$. Помогите понять, почему это так? Понятно, что верхнее состояние используется для счётчика $a,$ а верхний переход $b$ срабатывает только при наличии токена в состоянии под ним, то есть он предназначен для "повторения" нужного количества $b.$ Но ведь токен, попадающий в это состояние, может просто уйти в крайнюю вершину, и тогда получится слово не из языка. Я где-то не прав?

[Xaositect]

Вроде бы правы, но приведите определения того, как сеть функционирует, и как она порождает язык, которые у Вас в курсе были. Может там какие-нибудь мелочи есть, которые такого не позволяют

[cyb12]

Функционирование сети определялось стандартно. Порождение языка так: если взять последовательность $T_1,\ldots,T_k$ ($T_i$ -- переход, который сработал $i$-ым, после $k$-ого ничего не срабатывало) и по ней построить соответствующую последовательность $a_1,\ldots,a_k$ ($a_i$ -- пометка $T_i$), то $a_1a_2\ldots a_k$ -- слово порождаемого языка и язык состоит из всех возможных таких слов.

[Xaositect]

Ну тогда Вы правы, и порождается язык $\{a^nb^m | 1<m\leq n\}$. Он, впрочем, тоже КС.

[cyb12]

Обнаружил в книге Дж.Питерсона "Теория сетей Петри и моделирование систем" аналогичную схему и тем не менее, язык $\{a^nb^n\}$... Ещё не разбирался, но, возможно, там другое определение. Интересно, как можно ввести определения, чтобы порождался такой язык...