Читаю лекции Е.В.Троицкого, добрался до очередной теоремы. Всё было понятно, но вот в конце, после слова "итак"... Во-первых непонятно откуда всплыло предпоследнее уравнение, а во-вторых эти замены..там надо поворачивать, а не переносить. Ну вот я пытался поворачивать и подставлять в правильное уравнение, но получаются такие громоздкие выражения, что я с ними уже второй день вожусь. Может кто подскажет как сделать это полегче? Или ссылку даст на какой-нибудь материал с аналогичной теоремой. Заранее спасибо. Ниже текст теоремы:
Теорема 16.11. Коническая поверхность над эллипсом является конусом второго порядка.
Докозательство. Выберем такую систему координат с центром в О, что плоскость

задаётся уравнением

. Если мы выберем направления осей Ox и Oy параллельно главным осям эллипса, то уравнение эллипса в плоскости

(плоскости эллипса) примет вид:

, где

. Тогда уравнение конической поверхности над ним:

. Действительно, точка (x,y,z),

, принадлежит поверхности тогда и только тогда, когда точка

принадлежит кривой, т.е.

. Но при сделанном предположении

данное уравнение равносильно выводимому. Осталось доказать, что при

выводимое уравнение определено и его множество решений совпадает с О. Определённость следует из того, что во втором сомножителе степень

равна 2 и при умножении пропадает. После умножения уравнение превращается ( при

) в

. Поскольку ассимтотических направлений у эллипса нет, то x=y=0.
Итак,

. "вот оно всплывшее уравнение"
После замены
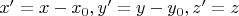
"вот эти странные замены" получаем

, т.е. конус.