диффур в банаховом пространстве

[terminator-II]

Привести пример банахова пространства $X$ и задачи Коши

$$\dot x=f(x)\in C(X,X),\quad x(0)=0$$

которая не имеет решения.

[Padawan]

$X=C[-1,1]$

$$\dot x(s)=s+{\mathrm {sgn} \; x(s)} \sqrt{|x(s)|}, \ \ \ x(s)(0)=0$$

Здесь ${\mathrm {sgn} \; x}$ -- знак $x$.
Предположим, что решение $x(s)(t)\in C[-1,1]$ существует. Заметим, что тогда $x(s)(t)\geqslant 0$ при $s>0$, и $x(s)(t)\leqslant 0$ при $s<0$.
Поэтому в точке $s=0$ , обязательно $x(0)(t)=0$.
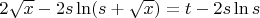
Если $s>0$, то решение такое $2\sqrt{x}-2s\ln(s+\sqrt{x})=t-2s\ln s$. Устремим здесь $s\to 0$ при фиксированном $t>0$ . Тогда по непрерывности должно быть $x(s)\to x(0)(t)=0$. Левая часть равенства стремится к $0$, правая - к $t>0$. Противоречие.

[terminator-II]

Здорово!

После того как первый пример такого сорта был изготовлен Годуновым в $c_0$ возник вопрос о том существуют ли такие системы в рефлексивных пространствах. Примеры тоже появились. Потом был построен пример и для гильбертова пространства. Точку опять поставил Годунов: теорема Пеано справедлива тогда и только тогда когда пространство конечномерно.