рассмотрим несколько иное уравнение:

,

,

и исследуем случаи
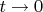
,

1)

2) для больших углов получается

,
читать Вас лично мне трудно.
Вы апеллируете к какому-то уравнению, содержащему

; а решение формулируете в терминах

. Надо бежать, листать старые сообщения, пытаться понять, что как с чем связано.
Вроде какая-то новая задача; её можно и нужно сформулировать без этих ссылок, компактно (self-contained).
Я также не умею с Вашей ловкостию анализировать асимптотику Д.У. Я бы мог перейти к указанным пределам, если бы видел пояснения или решение уравнения. Но как это сделать в самом Д.У. - не знаю. И мозк напрячь не особо получается. О ДУ я обычно беседую через посредство Камки.
Стоило бы написать, что понимается под спиралью Галилея (она не из тех, кого положено помнить наизусть).

,

А здесь и ро, и фи, и тэ... Непонятно...