(m) – Общее количество чисел на интервале (0,m)
p_n - простое число
(n) - номер простого числа
Q - Количество простых чисел на интервале (0,m)
E - Погрешность вычисления количества простых чисел на интервале(0,m)


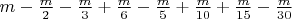
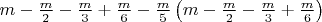
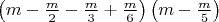
![$
\left[ {m - \frac{m}{2} - \frac{m}{3}\left( {m - \frac{m}{2}} \right)} \right]\left( {m - \frac{m}{5}} \right)
$ $
\left[ {m - \frac{m}{2} - \frac{m}{3}\left( {m - \frac{m}{2}} \right)} \right]\left( {m - \frac{m}{5}} \right)
$](https://dxdy-01.korotkov.co.uk/f/0/1/6/01601f1e41a7c28d5a770a4384e399ff82.png)
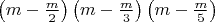
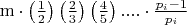
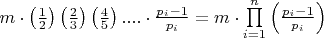
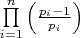
- формула вычисления результата решета Эратосфена
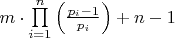
- Формула для вычисления количества простых чисел на интервале (0,m)
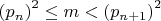
Погрешность вычисления количества простых чисел на интервале (0,m) при прохождении (m) значений
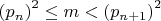
Изменяется от отрицательных значений к положительным. Общее направление изменения. Изменение погрешности вычисления внутри интервала, неравномерное со сменой направления, от отрицательных значений к положительным и обратно.
Эмпирическое значение (m) при котором погрешность вычисления меняет свой знак при изменении (n) такое
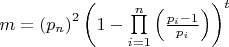
Увы значение (t) не имеет привязки к основным значениям формулы (пока что)
Что означает, значение (t) нужно определять исходя из вычисления и сравнения с данными таблицы простых чисел.
В этом значении (t) вся проблема работы и её незавершённость. А может значение (t) вобще не нужно, у меня нет возможности посчитать результат для больших чисел. С программой полная неувязка.
И всё же, даже те данные таблицы, которые мне доступны и мои результаты вычисления дают основания к некоторым выводам. Например:
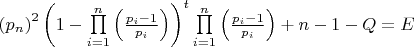
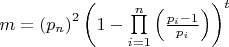
Поиск системы в изменениях погрешности, при вычислении количества простых чисел на интервалах, довольно занимательное занятие. Но я сосредоточился пока на поиске значений, при которых E = 0
Используя формулу
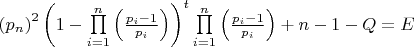
при (t=1)
я нашёл такие значения (m) при котором E=0 эти значения (m) находятся на переходе (E) от отрицательных значений к положительным и обратно. На одном переходе два значения (m).
Например:
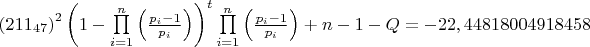
(m)=43122,85384902973) 43122,85384902973*0,1034022473468631+47-1=4505 Q=4505
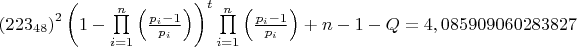
(m)=44375,98499367409) 44375,98499367409*0,1029385601390297+48-1= 4615 Q=4615