gris, Спасибо. Я не могу понять, как вывести синус из формулы.
Непонятки: в первом сообщении у Вас косинус -0.6, в последнем почему-то -0.16.
Извините, опечатался.
Синус икс неправильно вычислен в первом сообщении и перенесён в последнее.
А между тем, если Вы ту окружность нарисовли аккуратно циркулем, то Вы увидите, что синус равен ровно-точно восьми клеточкам:
Осталось это правильно-грамотно сосчитать.
-- Сб сен 25, 2010 14:30:59 --Удивляет, однако, что при этом палочки перед sin, cos в формулах типа

Вы ставите потрясающе грамотно!
Спасибо большое. Получается


Я прошу меня извинить, я еще не выработал навык. В системе КиМ освещено решение на основе выведения из формул, все задания решил, а в данном - решить не смог, т.к. не разобрался как найти
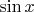
путем выведения из формулы. Спасибо.