Проверка нормальности при помощи критерия типа  0.
0. Пусть сл. в.

независимы и одинаково [в нашем случае (

)-нормально] распределены; область значений сл. в.

разбита на

-промежутков (классов). Введем обозначения:

,

— количество попаданий элементов выборки в

-ый промежуток,

;

— зависящая от неизвестных параметров вероятность попадания элемента выборки в

-ый промежуток;
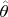
— мультиномиальная оценка максимального правдоподобия (м.о.м.п.) — оценка, максимизирующая функцию правдоподобия (или, что эквивалентно, логарифм функции правдоподобия) сгруппированных данных, т.е. такая оценка, что при

логарифм функции правдоподобия

достигает максимума.
По теореме Фишера, статистика

распределена, при

, как

, где

— число неизвестных скалярных параметров (в рассматриваемом случае их два:

,

). Основанный на данной статистике критерий (критерий Пирсона для параметрической гипотезы) используется, когда разбиение области значений случайной величины «задано до получения выборки».
1. Обозначим через

состоятельную оценку параметра

. На основе этой оценки зададим разбиение области значений случайной величины

. Обозначим, аналогичную

, статистику, построенную по этому случайному разбиению, через

, т.е.

. (1)
При выполнении некоторых условий на семейство распределений

по вероятности, при

(детали см. в [1]). Типичным примером применения критерия, основанного на статистике

, является такой. На основе статистики

задаётся разбиение, такое, что вероятность попадания в каждый интервал при

равна

. При заданном разбиении находят м.о.м.п. параметра

. Вычисляют статистику

и сравнивают с квантилью

соответствующего уровня

. Как и в критерии Пирсона для параметрической гипотезы, основную гипотезу отвергают, если

.
2. Для вычисления м.о.м.п. можно использовать метод накопления (scoring system) Фишера. (Краткие сведения об этом методе можно найти в [2]; применение метода для получения м.о.м.п. математического ожидания при известном стандартном отклонении и м.о.м.п. стандартного отклонения при известном математическом ожидании см. в [3]). Будем использовать обозначения
![$\Delta [f(t_j)] = f(t_j) - f(t_{j-1})$ $\Delta [f(t_j)] = f(t_j) - f(t_{j-1})$](https://dxdy-01.korotkov.co.uk/f/4/a/4/4a47d68b92f782e0cae07ce79cd78faa82.png)
,

,

— плотность стандартного нормального распределения,

— функция стандартного нормального распределения,

— столбец «накоплений» (иногда говорят «вкладов»).

,

. Обозначим матрицу информации для сгруппированных данных через

:
3. Для иллюстрации вышеизложенного были выполнены серии экспериментов для выборок объемов 30, 100, 200 и количестве промежутков 5 и 10. В каждой серии выполнялось 1000000 экспериментов состоящих из:
(i) генерирования выборки  (с параметрами
(с параметрами  ,
,  );
);
(ii) получения значения оценки 
,

, (3)
 ,
,  ,
,  — квантиль уровня
— квантиль уровня  стандартного нормального распределения;
стандартного нормального распределения;
(iv) вычисления м.о.м.п. по формуле (2) с использованием оценки (3) в качестве начального значения; (v) вычисления статистики (1) и сравнения с квантилью уровня  , которая выбиралась равной 0.80, 0.85, 0.90, 0.95, 0.99.
, которая выбиралась равной 0.80, 0.85, 0.90, 0.95, 0.99.
Первоначально, для того чтобы иметь возможность быстро выполнять длинные серии экспериментов, для вычисления функции распределения использовалась аппроксимация [4, п.7.1.26], которая имеет невысокую точность. Затем использовалась более точная аппроксимации из Cephes Math Library Release 2.8 (с максимальной погрешностью около

). Использование Cephes Math Library значительно улучшило сходимость.
Условие прекращения итераций
В таблице приведены результаты проверки гипотезы при различных

(вероятностях принять гипотезу, когда она верна: 0.80, 0.85, 0.90, 0.95)
Видно, что наблюдаемая частота принять гипотезу, когда она верна, хорошо соответствует номинальному уровню для выборки даже такого малого объема как 30.
Ссылки
1. Чибисов Д.М. Некоторые критерии типа

для непрерывных распределений // Теория вероят. и её примен., Т. XVI, выпуск 1, с. 3–20, 1971.
2. Рао С.Р. Линейные статистические методы и их применение. — М.: Наука, 1968.
3. Куллдорф Г. Введение в теорию оценивания. — М.: Наука, 1966.
4. Абрамовиц М., Стиган И. Справочник по специальным функциям. — М.: Наука, 1979.