Существование функции с интересным свойством

[Serge]

Известно, что не существует непрерывной всюду определенной функции $F:\mathbb{R}\to\mathbb{R}$ со свойством:
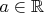
для любого $a\in\mathbb{R}$ уравнение $F(x)=a$ либо имеет ровно 2 различных решения, либо вовсе не имеет решений.

Вопрос: Что можно сказать об аналогичном отображении $F:\mathbb{R}^{2}\to\mathbb{R}^{2}$?
Т.е. существуют ли непрерывные всюду определенные функции двух действительных переменных $f:\mathbb{R}^{2}\to\mathbb{R}$ и $g:\mathbb{R}^{2}\to\mathbb{R}$,
такие, что для любых $a,b\in\mathbb{R}$ система уравнений $f(x,y)=a$, $g(x,y)=b$
либо имеет ровно 2 различных решения, либо вовсе не имеет решений?