Three points on a line

[ins-]

It is given a circle k and point P outside. PA and PB are the tangents from P to k. A line l through A parallel to PB intersects k at point C. Q is a point on k in different half-plane from P with respect to the line BC. D is the intersection point of BC and AQ. E is the intersection point of BQ and AC. Prove that D, E and P lies on a line.

[sergey1]

Пусть прямые $CQ $и $AB$ пересекаются в точке $Х$. Тогда $DE$ - поляра точки $Х$.Т.к. $Х$ лежит на $АВ$, то поляра $Х$ проходит через полюс $АВ$, поэтому $Р$ лежит на $DE$.

[ins-]

Is it possible to solve the problem without polars?

[gris]

Используя свойства вписанных углов и угла между касательной и хордой можно показать, что $\angle EDP=180^{\circ}$

[ins-]

Can you post the solution? I'm sorry I only ask for solutions and not think. I'm totally out of condition.

[Dimoniada]

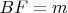
Пусть $AC=a$, $CE=b$, $EQ=c$, $QB=d$, $BF=m$, $FA=n$, где точка $F$ - пересечение $ED$ c $BA$. Тогда по т.Чевы из тр-ика $ABE$ имеем $m*a*c=n*b*d$ или $m/n=b*d/(a*c)$. Теперь, если мы хотим доказать, что точки $E$, $F$, $P$ лежат на одной прямой, то должно выполняться (и этого достаточно) $m/n=BP/(a+b)$. Значит, остаётся проверить равенство (*) $b*d/(a*c)=BP/(a+b)$, но по теор. о секущей $b*(a+b)=c*(c+d)$. Тогда (*) примет вид $d*(c+d)=BP*a$. Из подобия тр-иков $BPA$ и $BAC$ имеем $BP*a=BA^2=BC^2$. Осталось проверить, что $d*(c+d)=BC^2$, но это следует из подобия тр-иков $BCE$ и $BCQ$.

That's all

[ins-]

Wow! It is a cool solution. Greetings!

[ins-]

Indeed sergey1's solution is the shortest one I've seen. gris, if it is possible, can you explain in more details your idea?

[Dimoniada]

ins-, я объясняла вам решение без использования полярных преобразований, как вы и просили. А так, в принципе существует доказательство короче, чем привёл sergey1.

[ins-]

Какое это доказательство?


P.S.
I'm sorry. I learnt Russian 8 years in the school but I'm using at my workplace mostly Bulgarian and English. In the future I can try to use more Russian for easier communication. You will have lots of smileys probably if you want you can correct my sentences. Languages aren't my strongest side.

[Dimoniada]

Ваша задача - есть утверждение т. Паскаля для шестиугольника $AABBQC$.

[ins-]

Это очень плохо ... нет оригинальность.