Imperator писал(а):
Пусть

и

- два нечетных натуральных числа. Последовательность

определяется следующим образом:

,

а при


определяется как наибольший нечетный делитель

Докажите,
что для достаточно больших

значение

постоянно, и найдите это
значение как функцию от

и
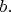
Очевидно, что все члены (являющиеся нечётными числами) не превосходят mаx(a,b) и максимум двух последующих не возрастающая последовательность, поэтому имеет предел , и этот предел является пределом для всей последовательности. Можно оценить и длину стабилизации, которая не превосходит квадрата от max(a,b).