Вычисление суммы ряда

[Konstantin84]

Уважаемые форумчане, при решении задачи по управлению запасами столкнулся с такой проблемой: необходимо найти сумму сходящегося ряда вида:
a/(b+1)! + (a^2)/(b+2)! + ... + (a^n)/(b+n)! при n-> к бесконечности. а и b - некоторые числа. Значение этой суммы необходимо чтобы посчитать формулу вероятности превышения спросом значения некоторого запаса. Поскольку в исходной задаче дело идет о дискретном запасе, то используется именно суммирование а не непрерывный интеграл.
Есть предположения, что эту сумму можно свести к разложению в ряд Маклорена экспоненты, но я не могу придумать как.

[lim0n]

А если вынести общий множитель

$$\frac {a}{b!}\sum\limits_{k=1}^{n}\frac {a^k}{b+k}$$

Пардон, сморозил...

[ИСН]

Тут философский вопрос: что лучше, конечный ряд или бесконечный?
(Это в случае, если Ваши "некоторые числа" - какие надо некоторые. Иначе всё плохо.)

-- Пн, 2010-08-16, 10:08 --

lim0n, не несите чушь.

[Konstantin84]

Вопрос может быть и философский, но конечность ряда для данной задачи не приемлема по той причине, что сумма в таком случае будет зависеть от параметров а, b и n. Мне же нужно выражение для суммы, независящее от n. Возможно если я распишу исходную задачу - это немного прояснит ситуацию?
Задача такая: задан некоторый случайный спрос предъявляемый к отдельному звену. Этот спрос имеет параметр интенсивности "лямбда". Сам спрос дискретный и составляет 1 единицу некоторой продукции. Получается что мы имеем Пуассоновский случайный поток с параметром "лямбда". За время Т величина спроса составит "лямбда"*Т. Вероятность того что спрос примет некоторое значение N на промежутке Т вычисляется по известной формуле для Пуассоновского потока P(N) = ((("лямбда"*T)^N)/N!)*exp^-"лямбда"*T - это все хорошо известно. Далее мне надо посчитать полную вероятность того что эта величина N превысит наш запас S на 1 единицу продукции, потом на 2, на 3 и т.д., то есть сумму вероятностей P(S+1)+P(S+2)+....и так далее. Отсюда и вытекает описанная мною задача, только я заменил произведение "лямбда"*T на букву а, а S+1 на b+1, чего в общем-то можно и не делать. Я знаю, что в материалах по СМО (системам массового обслуживания можно найти сумму вероятностей, но все эти формулы не для такой постановки задачи)

[mihailm]

Если параметры натуральные и умножим на a в степени b, то получится хвост экспоненты

[Konstantin84]

Блин, ну вот оно простое и изящное решение - спасибо, разобрался.

[Konstantin84]

Нет не решается задача. Я разобрался с комментарием ИСНа. Действительно, тот же самый вопрос получается при решении задачи:
$1+\lambda T+\frac{{(\lambda T)}^{2}}{2!}+...+\frac{{(\lambda T)}^{S}}{S!}= R*{e}^{\lambda T}$
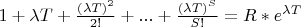
При заданном лямбда и Т найти величину S, чтобы выполнилось равенство, где R - это вероятность отсутствия дефицита в системе она задана и 0<R<1.
Вопрос существует ли формула чтобы выразить сумму любого количества членов ряда Маклорена для экспоненты через R, лямбда и Т, то есть решить это уравнение относительно S?

[AKM]

Konstantin84,

в Карантине, куда я временно переместил Вашу тему, Вы сможете отредактировать предыдущие свои сообщения, в плане написания формул по правилам. После редактирования напишите в тему Сообщение в карантине исправлено. Один из модераторов вернет тему в раздел «Помогите решить/разобраться (M)».