Решить реккурентное соотношение (через произв. функцию)


.
Составил ПФ, но не сходится с ответом. Я умножил второе уравнение на

, проссуммировал по
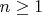
и сложил с первым уравнением. Получилось

Слева ---

, справа внутренняя сумма это свертка последовательности (1,2,3,..) (ПФ для нее

) с

, то есть получается

А в ответе

. Откуда взялся

в числителе?