Насчет литературы не скажу.
Тут было написано неочевидное утверждение.
Теперь по поводу вполне упорядочения. В нашем ЧУМ есть наибольший элемент - класс последовательностей, изоморфных натуральному ряду. Минимальных элементов нет. Далее, между любыми двумя классами
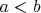
существует промежуточный класс: начиная с некоторого элемента

есть подпоследовательность

, причем множество

бесконечно (иначе

), поэтому, добавив к

любую собственную подпоследовательность последовательности

, получим искомый промежуточный элемент.
То есть существует счетная цепь, которая является плотное линейное упорядочение без макс. и мин. элементов. Это порядковый тип

рациональных чисел. Напомню, что в

можно вложить любое не более чем счетное упорядоченное множество.
-- Пт июн 25, 2010 13:42:25 --Так, написал я про счетность цепей и задумался, а правда ли это Конечно, неправда.