Z_2-индекс

[Solunac]

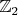
(The $\mathbb{Z}_2$ index is the largest among "reasonable" index functions - P.E. Conner and E. F. Floyd. Fixed point free involutions and equivariant maps. Bull. Amer. Math. Soc., 66:416-441, 1960.)
Problem: Let $\chi$ be a family of metric free $\math{Z}_2$-spaces with $(S^0, -)\in\chi$ and such that if $X\in\chi$ and $A $ is a closed invariant subset of $X$, then $A\in\chi$. Let $I:\chi\mapsto\{0,1,2,\ldots\}\cup\{\infty\}$ be a function satisfying, for all $X, Y\in\chi$:
(i) If $X\mapsto Y$, then $I(X)\leqslant I(Y)$.
(ii) If $X=A\cup B$ for closed invariant sets $A$ and $B$, then $I(X)\leqslant I(A)+I(B)+1$.
(iii) $I(S^0)=0$.

Prove that $I(X)\leqslant ind_{\mathbb{Z}_2}(X)$ for all $X\in\chi$.

Thanks in advance.