Ортогональные наборы целых чисел.

[Imperator]

Пусть $a$, $b$, $c$ и $R$ - целые числа, удовлетворяющие соотношению $a^{2}+b^{2}+c^{2}=R^{2}.$
Решить в целых числах систему
$ \left\{ \begin{array}{l} x^{2}+y^{2}+z^{2}=R^{2},\\ ax+by+cz=0. \end{array} \right. $

[незваный гость]

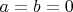
А как Вы представляете себе решение? рассмотрим простейший случай: $a=b=0$, $c=R$. Тогда система сводится к решению в целых числах уравнения $x^2+y^2=R^2$. Помимио тривиальных решений, у него мжет быть произвольное число нетривиальных (в зависимости от $R$).

Произвольность их числа можно показать, например, так: для произвольной несократимой пифагоровой тройки $p, q, r$, $p^2+q^2=r^2$ имеем решение $x = R\frac{p}{r}$, $y = R\frac{q}{r}$, если $r$ делит $R$. Выбирая $R$ как наименьшее общее кратное нужного числа $r_i$ имеем (конструктивно) нужный результат.

Вопрос -- какой ответ Вы ждете?

[Руст]

Ясно, что количество решений зависит от разложения числа R. Кроме этого случая, легко предъявить все решения и в случае, когда среди чисел a,b,c два из них равны по абсолютной величине. Можно показать, что решение всегда имеется и количество решений делится на 4.

[Руст]

Целые точки в трёхмерном пространстве (можно представить как чисто мнимые кватернионы), а их подмножество на плоскости, ортогональной к вектору (a,b,c) образуют решётку (вообще говоря уже не ортогональную). Задача сводится к нахождению пересечения этой решётки с окружностью. Его можно переформулировать как нахождению целых чисел квадратичного расширения K=Z[x] с заданной нормой или представлению числа R в квадрате квадратичной формой. Эти задачи алгоритмический решаются и имеются в курсах теории чисел. Однако, не имеют явного красивого ответа в общем случае. Может я ошибаюсь и вы дадите (не найденное нами) красивое решение.